Heap Sort
Heap Sort,中文有堆積排序或累堆排序。
使用完整二元樹與陣列建立堆積樹與排序。
完整二元樹
完整二元樹(Complete Binary Tree),由上而下由左而右(參考下圖箭頭方向),中間不會有空缺,逐一把節點一個一個放入陣列中。
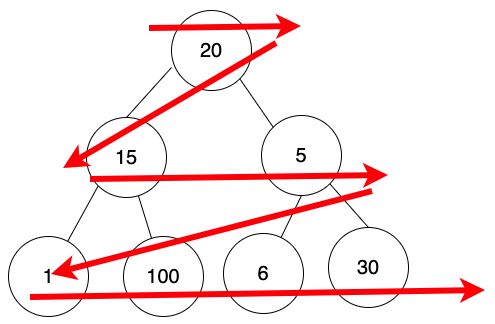
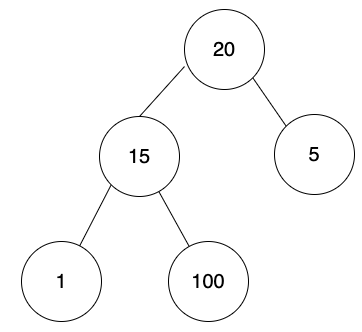
對映的陣列如下:
[20, 15, 5, 1, 100]
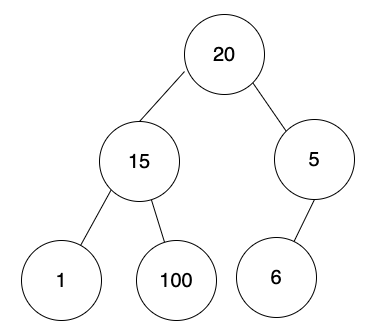
對映的陣列如下:
[20, 15, 5, 1, 100, 6]
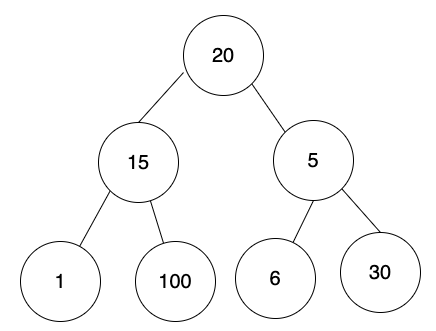
對映的陣列如下:
[20, 15, 5, 1, 100, 6, 30]
若中間有空缺,就不是完整二元樹。
以下缺少第二層的右子樹,不是完整二元樹。
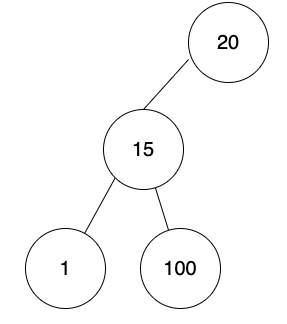
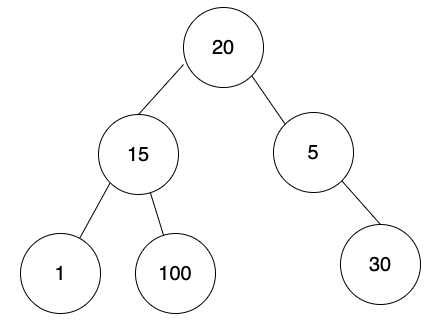
以下有少一個節點,有空缺,不是完整二元樹。
陣列索引與樹
下圖,加上對映的陣列索引。
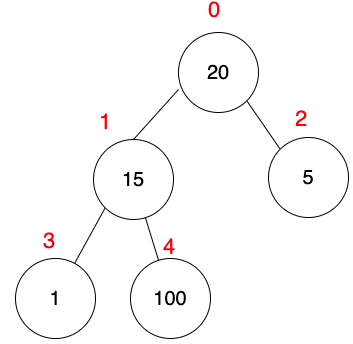
陣列:
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 15 | 5 | 1 | 100 |
左子節點公式,i為「父」節點索引。
2 * i + 1
右子節點公式,i為「父」節點索引。
2 * i + 2
找出父節點公式,i為「子」節點索引。
(i - 1) / 2
假如我們要找父節點索引為1,值是15,它的左右子節點,要如何找?
左子節點
2 * 1 + 1 = 3
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 15 | 5 | 1 | 100 |
右子節點
2 * 1 + 2 = 4
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 15 | 5 | 1 | 100 |
找出索引為4的父節點,無條件去掉小數點。
(4 - 1) / 2 = 1
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 15 | 5 | 1 | 100 |
最大堆積樹與最小堆積樹
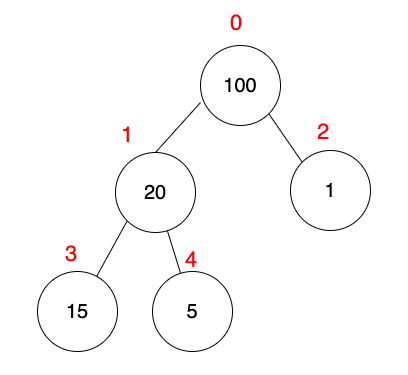
最大堆積樹
根節點都比左右子樹大。
最小堆積樹
根節點都比左右子樹小。
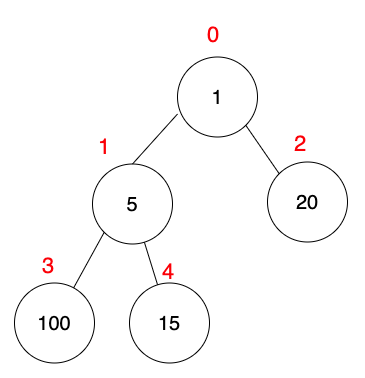
建立最大堆積樹
最大堆積樹由下往上,把最大值搬到根節點。
所以以下步驟由下往上找。
最後一個非葉子父節點
下圖中,索引1,值為15,就是最後一個非葉子父節點。
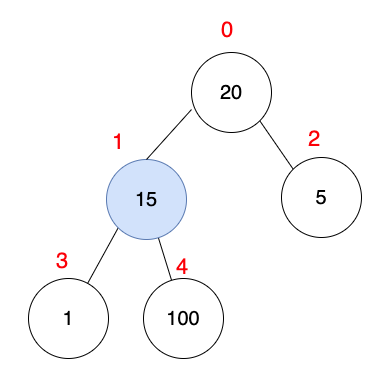
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 15 | 5 | 1 | 100 |
方法1:最後一個葉子的父節點
先前有提過找到「子」索引的父節點。
(i - 1) / 2
陣列中的最後一個元素,一定是葉子節點,可透過它來找父節點。
以下公式為「整數」除法,無條件捨去小數。
(arr.length - 1 - 1) / 2
(5 - 1 - 1) / 2 = 1
方法2:陣列大小/2 - 1
陣列大小除2,左半邊都是父節點,右半邊都是子節點。
陣列大小5除2 = 2,小於2不包含2都是左半邊,左半邊都是父節點,大於等於2,右半邊都是子節點。
| 父或葉子 | 父 | 父 | 葉 | 葉 | 葉 |
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 15 | 5 | 1 | 100 |
如果要取得最後一個父節點,也就要把陣列大小/2,再減1,就會取得最後一個父節點。
(arr.length / 2) - 1
(5 / 2) - 1 = 1
| 父或葉子 | 父 | 父 | 葉 | 葉 | 葉 |
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 15 | 5 | 1 | 100 |
左右子節點比父節點大就交換。
- 左右子節點先比較誰比較大
- 比較大的子節點,再跟父節點比大小,若子節點比父節點大,就交換。
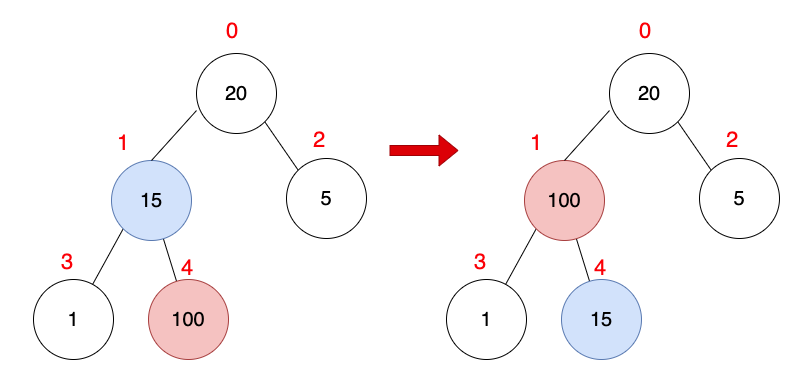
| 父或葉子 | 父 | 父 | 葉 | 葉 | 葉 |
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 100 | 5 | 1 | 15 |
倒數第二個父節點
先前有提過,陣列大小/2 = 第一個葉子節點,陣列大小/2,左半邊都是父節點,右半邊都是葉子節點。
剛才處理完最後一個父節點,索引為1,請問倒數第2個父節點怎麼求?
也就是索引1 - 1 = 0 ,就會得到倒數第2個父節點,索引為0。
| 父或葉子 | 父 | 父 | 葉 | 葉 | 葉 |
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 20 | 100 | 5 | 1 | 15 |
索引0,先看左右子節點有沒有比索引0的值大,有的話就交換。
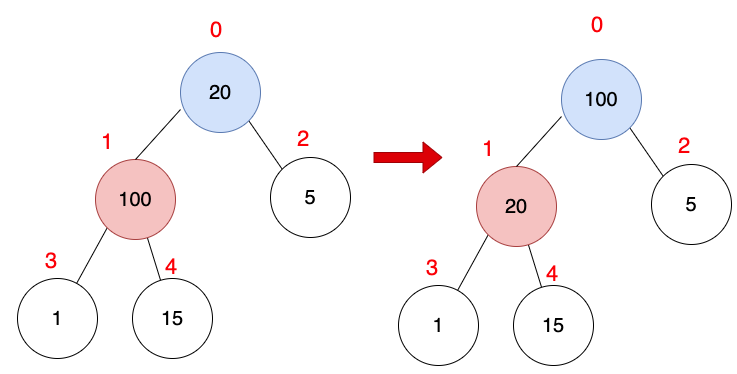
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 100 | 20 | 5 | 1 | 15 |
目前最大堆積樹已完成。
迴圈處理,「最後一個」非葉子節點與「倒數第2個」非葉子節點。
1
2
3
4
// 先從最後一個非葉子節點建立最大堆積樹
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjust(arr, i , arr.length);
}
陣列由小到大排序
要讓陣列由小到大排序,最大的要放最後面。
把根節點放在陣列最後一個索引位置
索引0的值為最大,要放最後面。
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 100 | 20 | 5 | 1 | 15 |
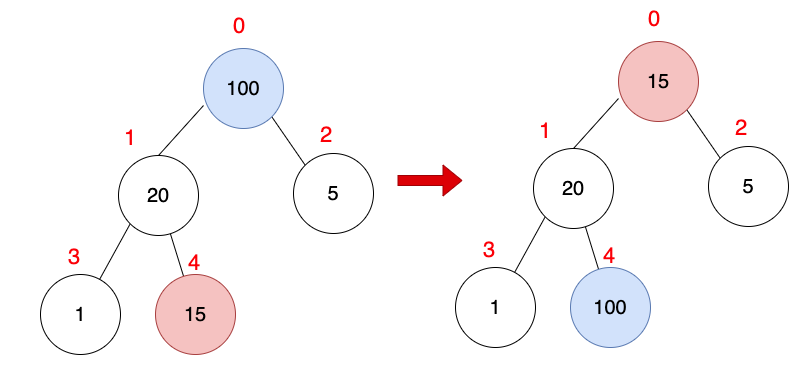
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 數值 | 15 | 20 | 5 | 1 | 100 |
把最後一個節點排除掉。
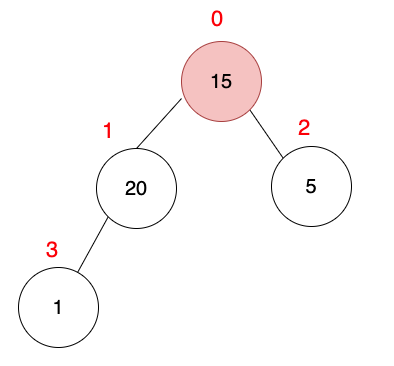
| 索引 | 0 | 1 | 2 | 3 |
| 數值 | 15 | 20 | 5 | 1 |
以下程式碼處理把最大arr[0]放在陣列最後面,然後注意是i>0,也就是i=0剩下一個,就不做了,因為都已經排序完畢。
1
2
3
4
5
6
7
8
9
for (int i = arr.length - 1; i > 0 ; i--) {
// 索引0的值為最大,要放最後面,交換
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
// i每次都少1個,形式上就是排除最後一個節點。
// 最後一個節點不處理
adjust(arr, 0, i);
}
重新調整最大堆積樹
從索引0根節點開始,去調整最大堆積樹,根節點要為最大。
i變數,指向根節點,目前i = 0
temp變數,暫存i變數指向的值,temp = 15。
1
int temp = arr[i];
k變數,指向比較大的左或右子節點,目前k = 1。
1
2
// k變數一開始指向左子節點
int k = i * 2 + 1;
1
2
3
4
5
若右子節點大於左子節點
if (k + 1 < len && arr[k] < arr[k + 1]) {
// k變數變右子節點
k++;
}
temp = 15 小於 arr[k = 1]。
arr[i = 0]位置放入arr[k = 1]。
i = ki與k指向同一個位置,i = k = 1。
1
2
3
4
if (temp < arr[k]) {
arr[i] = arr[k];
i = k;
}
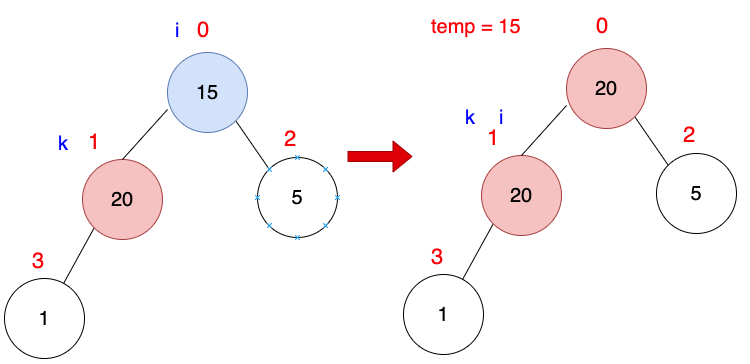
下一次迴圈,k++,k = 2。
arr[k = 2] = 5 沒有大於temp = 15,直接跳離迴圈。
1
2
3
4
5
6
7
if (temp < arr[k]) {
arr[i] = arr[k];
i = k;
} else {
// 執行以下這行
break;
}
此時已經找到15要插入的位置,i = 1,把temp=15放入arr[i = 1]。
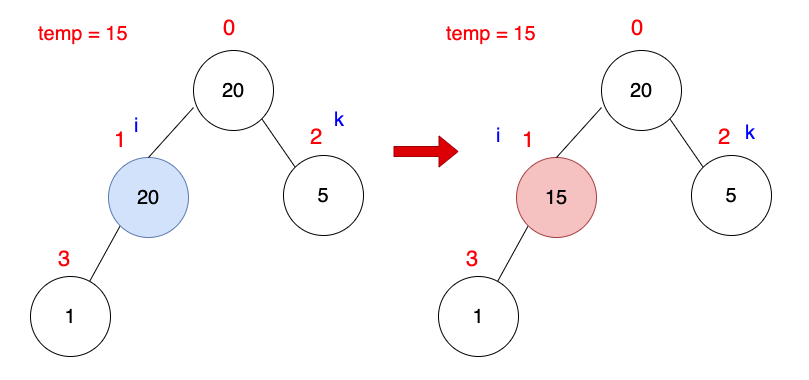
1
arr[i] = temp;
目前最大堆積樹已完成。
| 索引 | 0 | 1 | 2 | 3 |
| 數值 | 20 | 15 | 5 | 1 |
調整最大堆積樹的程式碼:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static void adjust(int[] arr, int i, int len) {
int temp = arr[i];
for (int k = i * 2 + 1; k < len; k++) {
if (k + 1 < len && arr[k] < arr[k + 1]) {
k++;
}
if (temp < arr[k]) {
arr[i] = arr[k];
i = k;
} else {
break;
}
}
arr[i] = temp;
}
把根節點放在陣列最後一個索引位置
索引0的值為最大,要放最後面。
| 索引 | 0 | 1 | 2 | 3 |
| 數值 | 20 | 15 | 5 | 1 |
| 索引 | 0 | 1 | 2 | 3 |
| 數值 | 1 | 15 | 5 | 20 |
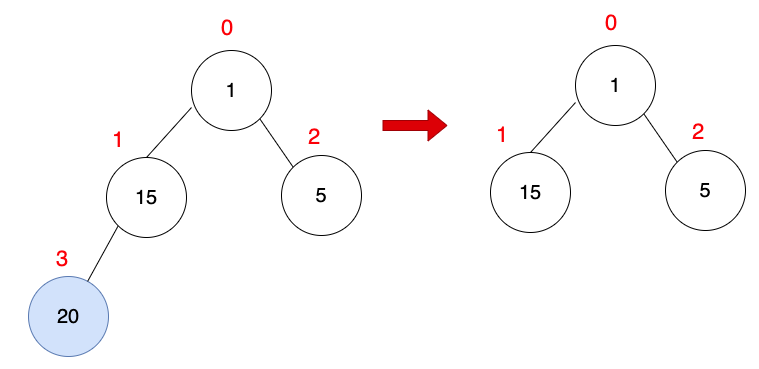
調整成最大堆積樹
i變數,指向根節點,目前i = 0
temp變數,暫存i變數指向的值,temp = 1。
k變數,指向比較大的左或右子節點,目前k = 1。
temp = 1 小於 arr[k = 1] = 15。
arr[i = 0]位置放入arr[k = 1]。
i = ki與k指向同一個位置,i = k = 1。
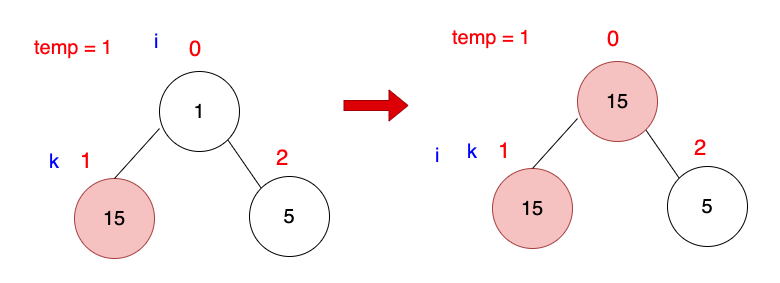
下一次迴圈,k++,k = 2,i = 1
temp = 1 小於arr[k = 2] = 5。
arr[i = 1]位置放入arr[k = 2]。
i = ki與k指向同一個位置,i = k = 2。
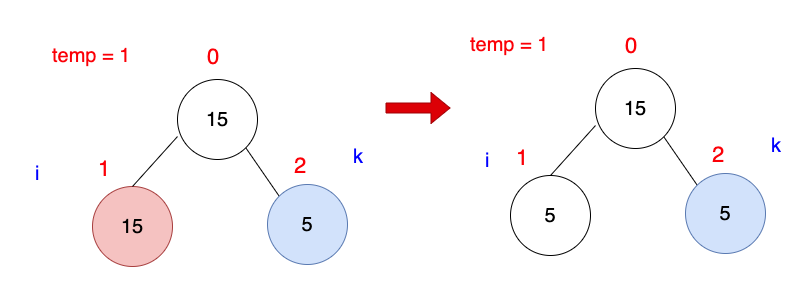
此時已經找到1要插入的位置,i = 2,把temp=1放入arr[i = 2]。
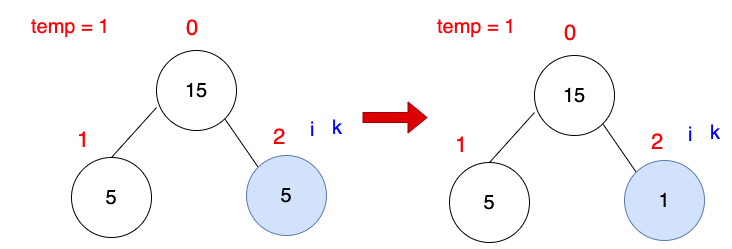
目前最大堆積樹已完成。
重覆調整的次數
重覆調整的次數為陣列大小 - 1。
完整程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class HeapSort {
public static void main(String[] args) {
// 要排序的陣列
int[] arr = {20, 15, 5, 1, 100};
// 前序遍歷
preOrder(0, arr);
// 先從最後一個非葉子節點建立最大堆積樹
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjust(arr, i , arr.length);
}
for (int i = arr.length - 1; i > 0 ; i--) {
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
adjust(arr, 0, i);
}
System.out.println(Arrays.toString(arr));
}
public static void adjust(int[] arr, int i, int len) {
int temp = arr[i];
for (int k = i * 2 + 1; k < len; k++) {
if (k + 1 < len && arr[k] < arr[k + 1]) {
k++;
}
if (temp < arr[k]) {
arr[i] = arr[k];
i = k;
} else {
break;
}
}
arr[i] = temp;
}
public static void preOrder(int i, int[] arr) {
System.out.print(arr[i] + ",");
if (i * 2 + 1 < arr.length) {
preOrder(i * 2 + 1, arr);
}
if (i * 2 + 2 < arr.length) {
preOrder(i * 2 + 2, arr);
}
}
}