118,119 Pascal's Triangle
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
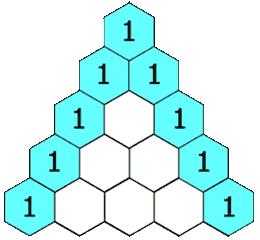
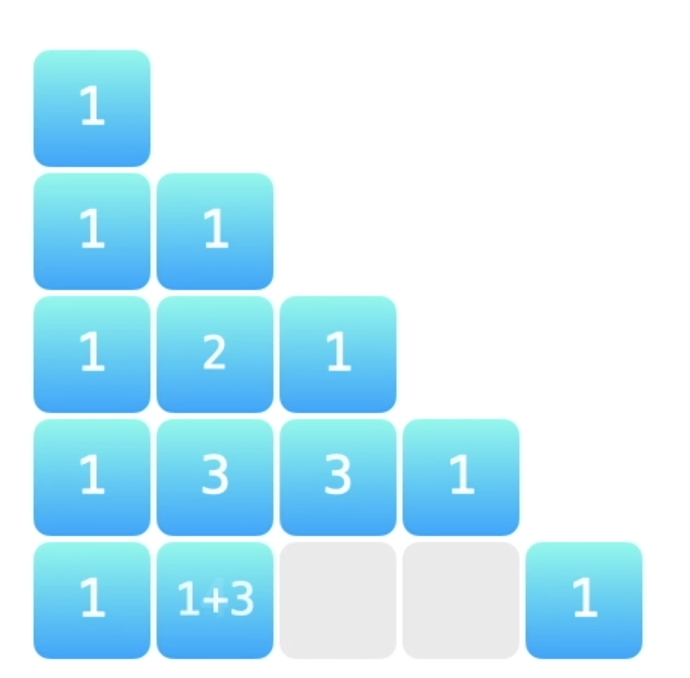
注意!index是由1開始 示例 1: 输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]] 示例 2:
输入: numRows = 1 输出: [[1]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList<>();
res.add(new ArrayList<>());
res.get(0).add(1);//先建立第一層1
for(int i = 2; i <= numRows; i++) {//從第二層依序到numRows,注意!這邊是小於等於,如果少了等於,就會少建一層
//注意,這邊是res.size()-1取出最後的res,不是i-1,因為初始時res只有一層,也就是res.get(0),若用i-1,i=2的時候,res.get(2-1)是會造成Array out of boundry
List list = generateRow(res.get(res.size()-1), i);
res.add(list);
}
return res;
}
private List<Integer> generateRow(List<Integer> prevRow, int numRows) {
List<Integer> list = new ArrayList<>();
list.add(1);//第一欄添加1
//注意,numRows等於2的時候,以下for loop不會進入因為 j = 1 , 1 不小於(2-1),直接到list.add(1)
for(int j = 1; j < numRows - 1; j++) {
list.add(prevRow.get(j-1) + prevRow.get(j));//前一個row的上一欄與同欄相加。
}
list.add(1);//最後一欄添加1
return list;
}
}
這段程式碼是用來生成帕斯卡三角形(Pascal’s Triangle)的,時間複雜度為 O(n^2),空間複雜度為 O(n^2)。以下是詳細的分析:
時間複雜度分析:
外層迴圈執行 numRows 次,內層迴圈執行 numRows - 1 次,所以總共執行次數為 (1 + 2 + … + numRows) * (numRows - 1) = numRows^2 - numRows,因此時間複雜度為 O(n^2)。
空間複雜度分析:
程式中建立了一個二維的 List,用來存儲帕斯卡三角形,大小為 numRows * numRows,因此空間複雜度為 O(n^2)。
遞迴寫法 注意!index是由1開始。所以終止條件為numRows == 1 注意!list.add(1)在終止條件增加一次,再做新的row, 也要再添加一次list.add(1); 是因為假設第3層,會跑i= 1 到 i = 2 (3-1) 输入: numRows = 1 输出: [[1]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList<>();
generateRow(res, numRows);
return res;
}
private List<Integer> generateRow(List<List<Integer>> res, int numRows) {
ArrayList<Integer> list = new ArrayList<>();
if(numRows == 1) {
list.add(1);
res.add(list);
return list;
}
list.add(1);
List<Integer> prevRow = generateRow(res, numRows - 1);
for(int i = 1; i < numRows - 1; i++) {
list.add(prevRow.get(i - 1) + prevRow.get(i));
}
list.add(1);
res.add(list);
return list;
}
}
注意!不能寫成以下方式,因為它只把[1, 4, 6, 4, 1] ,存到res,但實際上,每一次遞迴所產生的 list如下: [1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1] 必須在return前把生成的list存在res
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList<>();
res.add(generateRow(numRows));
return res;
}
private List<Integer> generateRow(int numRows) {
ArrayList<Integer> list = new ArrayList<>();
if(numRows == 1) {
list.add(1);
return list;
}
list.add(1);
List<Integer> prevRow = generateRow(res, numRows - 1);
for(int i = 1; i < numRows - 1; i++) {
list.add(prevRow.get(i - 1) + prevRow.get(i));
}
list.add(1);
return list;
}
}
時間複雜度分析: generate() 方法中,調用了 generateRow() 方法 numRows 次,每次 generateRow() 方法的時間複雜度是 O(numRows),因為每次都要遞歸呼叫 numRows - 1 次,並且在 for 迴圈中遍歷 numRows - 1 次,所以 generate() 方法的時間複雜度為 O(numRows^2)。
空間複雜度分析: generate() 方法中,創建了一個大小為 numRows 的二維動態數組 res,所以 generate() 方法的空間複雜度為 O(numRows^2)。同時,generateRow() 方法中也使用了遞歸,但每次只創建了一個大小為 numRows 的一維動態數組 list,所以 generateRow() 方法的空間複雜度為 O(numRows)。
另一個遞歸寫法(我覺得比較好),直接回傳List<List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList<>();
if(numRows == 1) {
res.add(Arrays.asList(new Integer[]{1}));
return res;
}
res = generate(numRows - 1);//抓前面的所有資料
List<Integer> prevRow = res.get(res.size() - 1);//抓最後一筆row的資料
List<Integer> newRow = new ArrayList<>();
newRow.add(1);
for(int i = 1; i < numRows - 1; i++) {
newRow.add(prevRow.get(i - 1) + prevRow.get(i));
}
newRow.add(1);
res.add(newRow);
return res;
}
在這個程式碼中,我們使用遞迴來產生帕斯卡三角形,而這個遞迴函數的執行次數是 numRows,因為我們要生成 numRows行的帕斯卡三角形。對於每一行,我們需要執行 i 次運算,其中 $i$ 是當前行的行號。因此,總的運算次數為:
因此時間複雜度是 O(numRows^2)。
需要注意的是,在這個遞迴函數中,我們建立了一個列表來存儲結果,因此空間複雜度也是 O(numRows^2)。
為什麼空間複雜度是O(numRows^2),是因為LIst中又在存List嗎 是的,空間复杂度是因为在每一行都存储了一个长度为该行元素个数的列表,而该列表中又存储了该行所有的元素。因此,列表的总长度为1+2+…+numRows,即n*(n+1)/2,也就是O(numRows^2)。
- Pascal’s Triangle II 注意!rowIndex是由0開始 Example 1:
Input: rowIndex = 3
Output: [1,3,3,1]
Example 2:
Input: rowIndex = 0
Output: [1]
Example 3:
Input: rowIndex = 1
Output: [1,1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public List<Integer> getRow(int rowIndex) {
List<Integer> list = new ArrayList<>();
if(rowIndex == 0) {//rowIndex是由0開始
list.add(1);
return list;
}
List<Integer> preRow = getRow(rowIndex - 1);
list.add(1);
//rowIndex為1的時候不會進入以下for loop
for(int i = 1; i < rowIndex; i++) {
list.add(preRow.get(i - 1) + preRow.get(i));
}
list.add(1);
return list;
}
}