BST新增
左子樹小於根節點,右子樹大於根節點。
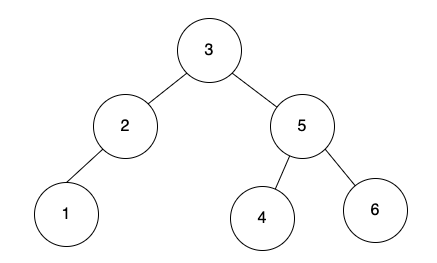
中序遍歷
中序的方式來遍歷樹,是由小到大,因為左子樹小於根節點,右子樹大於根節點。
新增
判斷root是否為空
新增的時候要判斷,若樹為空,直接把新增節點作為root根節點。
判斷大小
若樹不為空,判斷新增節點是小於根節點還是大於根節點。
小於根節點,判斷左子樹是否為null,若為null,就把新節點接上左子樹。
若左子樹不是null,繼續往左子樹找適合的位置來新增。
大於根節點,判斷右子樹是否為null,若為null,就把新節點接上右子樹。
若右子樹不是null,繼續往右子樹找適合的位置來新增。
建立二個類別,分別為class Node ,與class BinarySearchTree 。
Node處理非root的新增。
BinarySearchTree處理root節點的新增。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
public class BSTree {
public static void main(String[] args) {
BinarySearchTree binarySearchTree = new BinarySearchTree();
binarySearchTree.add(new Node(10));
binarySearchTree.add(new Node(5));
binarySearchTree.add(new Node(12));
binarySearchTree.add(new Node(20));
binarySearchTree.add(new Node(18));
binarySearchTree.inOrder();
}
}
class BinarySearchTree {
private Node root;
public void add(Node node) {
if (root == null) {
// 如果是空樹,就把根節點設為node
root = node;
} else {
// 如果不是空樹,就去子樹找,找到可新增的位罝
root.add(node);
}
}
public void inOrder() {
if (root != null) {
root.inOrder();
}
}
}
class Node {
int id;
Node left;
Node right;
public Node(int id) {
this.id = id;
}
@Override
public String toString() {
return "id=" + id ;
}
public void inOrder() {
if (this.left != null) {
this.left.inOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.inOrder();
}
}
public void add(Node node) {
if (node == null) return;
// 小於新增在左子樹
if (node.id < this.id) {
// 左子樹是葉子節點,才新增
if (this.left == null) {
this.left = node;
} else { // 不是葉子,就繼續往左子樹找
this.left.add(node);
}
} else {
// 大於、等於,新增在右子樹
// 右子樹是葉子節點,才新增
if (this.right == null) {
this.right = node;
} else { // 不是葉子,就繼續往右子樹找
this.right.add(node);
}
}
}
}