BST刪除
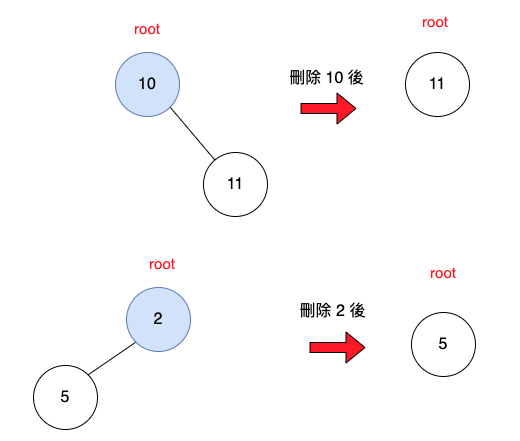
root節點刪除
root沒有子樹
直接把root設為null
root有一邊是有子樹,另一邊是null
如果root只有右子樹,要刪除root,直接把root指向右子樹。
如果root只有左子樹,要刪除root,直接把root指向左子樹。
root下二邊都有子樹
直接使用子節點刪除,要刪除的節點有2個子節點。
子節點刪除
單向鏈結串列刪除時,要先找到刪除節點的前一個節點,因為單向鏈結串列無法往回走。
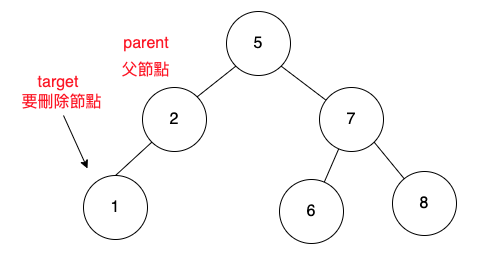
樹的刪除也是一樣,要先找到「要刪除節點」的「父節點」。
「要刪除節點」的「父節點」,命名為parent。
「要刪除節點」,命名為target。
名詞解釋
parent
parent為「要刪除節點」的「父節點」。
parent.left為「要刪除節點」的「父節點」下的左子樹。
target
「要刪除節點」,命名為target。
target.left為要刪除節點的左子樹。
target.right為要刪除節點的右子樹。
target = null
target為要刪除的節點。
使用target = null,無法刪除節點,因為方法中,區域變數taget修改成null,受影嚮的只有區域變數的target。
正確作法,使用要刪除節點target的父節點parent來刪除左子樹或右子樹。
1
2
parent.left = null;
parent.right = null;
葉子節點刪除
要刪除的節點是葉子,檢查要刪除的節點是左子節點,還是右子節點。
直接設為null。
要刪除的節點是左子節點,parent為「要刪除節點」的「父節點」。

1
parent.left = null;
要刪除的節點是右子節點,parent為「要刪除節點」的「父節點」。
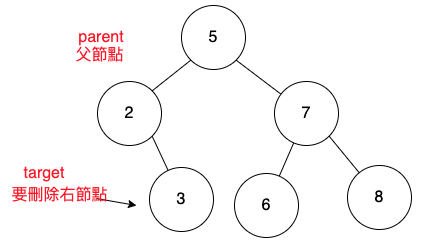
1
parent.right = null;
要刪除的節點,是左子節點,下面有子樹。
如下圖,要刪除的節點,是左子節點,下面有子樹。
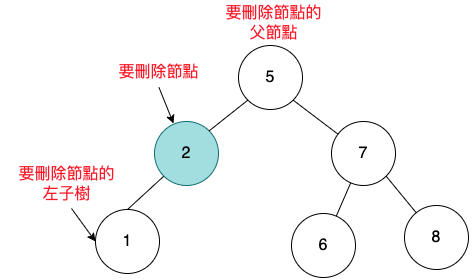
要刪除的節點,是左子節點,下面有一個左子樹。
刪除後的圖如下:
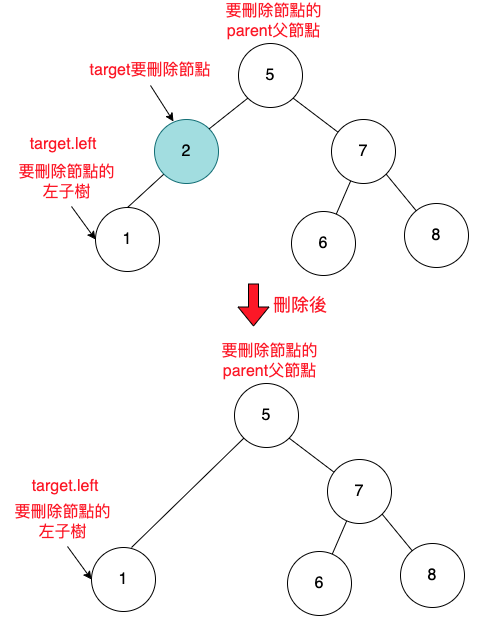
1
parent.left = target.left;
要刪除的節點,是左子節點,下面有一個右子樹。
刪除後的圖如下:
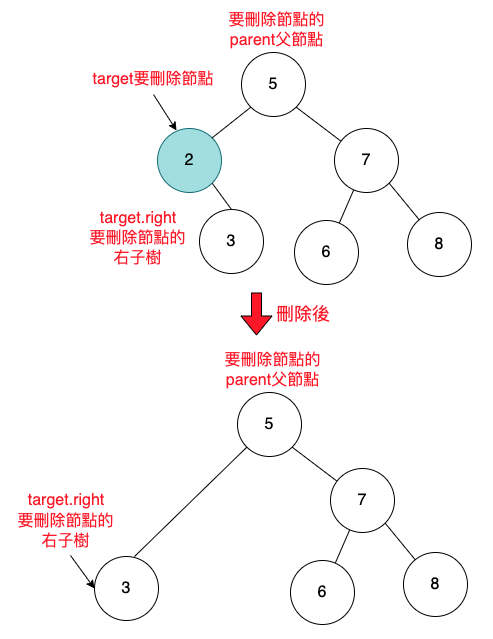
1
parent.left = target.right;
要刪除的節點,是右子節點,下面有一個子樹
要刪除的節點,是右子節點,下面有一個左子樹。
刪除後的圖如下:
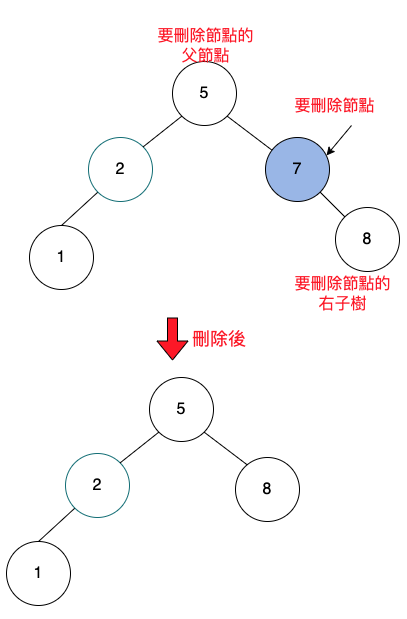
1
parent.right = target.left;
要刪除的節點,是右子節點,下面有一個右子樹。
刪除後的圖如下:
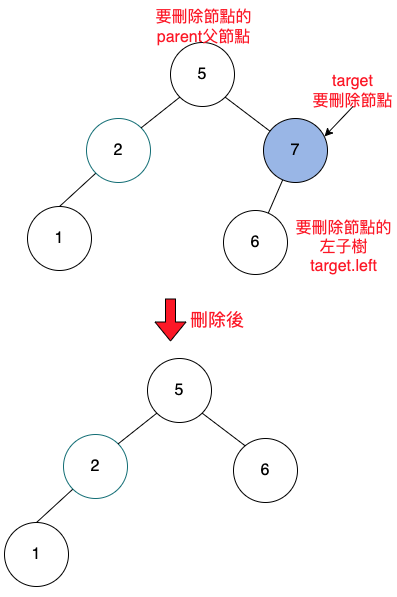
1
parent.right = target.right;
要刪除的節點有2個子樹
尋找右子樹中最小值,使用temp變數,暫存最小值。
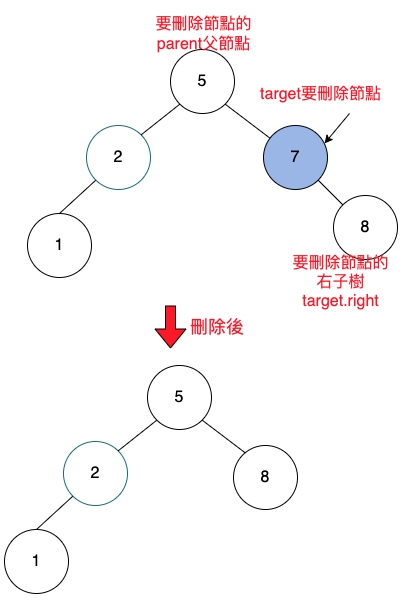
把最小節點8刪掉。
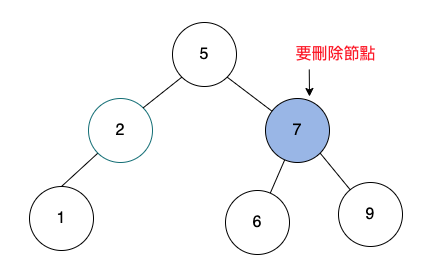
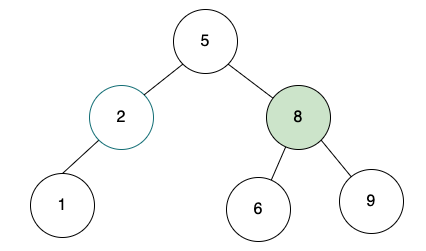
把要刪除節點的值,修改成temp變數最小值。
程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
public class BSTree {
public static void main(String[] args) {
BinarySearchTree binarySearchTree = new BinarySearchTree();
binarySearchTree.add(new Node(10));
binarySearchTree.add(new Node(5));
binarySearchTree.add(new Node(12));
binarySearchTree.add(new Node(11));
binarySearchTree.add(new Node(20));
binarySearchTree.add(new Node(18));
binarySearchTree.inOrder();
System.out.println("刪除後");
binarySearchTree.delNode(18);
binarySearchTree.delNode(20);
binarySearchTree.delNode(5);
binarySearchTree.delNode(10);
binarySearchTree.delNode(11);
binarySearchTree.delNode(12);
binarySearchTree.inOrder();
}
}
class BinarySearchTree {
public Node root;
public void add(Node node) {
if (root == null) {
// 如果是空樹,就把root設為node
root = node;
} else {
// 如果不是空樹,就去找子樹,可新增的位罝
root.add(node);
}
}
public void inOrder() {
if (root != null) {
root.inOrder();
}
}
public void delNode(int findValue) {
if (root == null) return;
Node target = findTarget(findValue);
// 找不到要刪除的節點,返回
if (target == null) return;
// root就是要刪除的節點,而且root左子樹與右子樹都是NULL
if (root == target && root.left == null && root.right == null) {
// 設為NULL
root = null;
// 返回
return;
}
// 尋找要刪除節點的父節點
Node parent = findParent(findValue);
// 要刪除的是根節點,根節點沒有parent,但根節點下面左子樹或右子樹,有一邊是NULL,有一邊是有子樹
// 例:10,11 要刪除10根節點,但10下面有11這個右子樹
// 直接把11這個右子樹取代root
// 例:2,5 要刪除5根節點,但5下面有2這個左子樹
// 直接把2這個左子樹取代root
if (parent == null && root == target && (root.right == null || root.left == null)) {
if (root.left == null) {
root = root.right;
} else {
root = root.left;
}
// 返回
return;
}
// 要刪除的節點是葉子
if (target.left == null && target.right == null) {
// 判斷父節點的左子樹是否為要刪除的節點
if(parent.left != null && parent.left.id == target.id) {
// 若是葉子,直接設成NULL
parent.left = null;
// 判斷父節點的右子樹是否為要刪除的節點
} else if (parent.right != null && parent.right.id == target.id) {
// 若是葉子,直接設成NULL
parent.right = null;
}
// 左子樹與右子樹不為NULL
} else if (target.left != null & target.right !=null) {
// 尋找右子樹中,最小值(從右子樹下的左子樹一路尋找)
int min = delRightTreeMin(target.right);
if (min != -1) {
target.id = min;
}
} else {// 若要刪的節點不為葉子,且左子樹或右子樹有一邊是NULL
// 要刪除節點target是在parent的左子樹
if (parent.left != null && parent.left.id == target.id) {
// 要刪除的節點下面有左子樹
if (target.left != null) {
parent.left = target.left;
} else {//要刪除的節點下面有右子樹
parent.left = target.right;
}
// 要刪除節點target是在parent的右子樹
} else if (parent.right != null && parent.right.id == target.id) {
// 要刪除的節點下面有左子樹
if(target.left != null) {
parent.right = target.left;
} else {//要刪除的節點下面有右子樹
parent.right = target.right;
}
}
}
}
public int delRightTreeMin(Node node) {
int min = -1;
while (node.left != null) {
node = node.left;
}
min = node.id;
delNode(node.id);
return min;
}
public Node findTarget(int target) {
// 如果ROOT為NULL,就直接傳回NULL
if (root == null) {
return null;
} else {
// 尋找要搜尋目標
return root.findTarget(target);
}
}
public Node findParent(int target) {
// 如果ROOT為NULL,就直接傳回NULL
if (root == null) {
return null;
} else {
// 尋找要搜尋目標的父節點
return root.findParent(target);
}
}
}
class Node {
int id;
Node left;
Node right;
public Node(int id) {
this.id = id;
}
public Node findTarget(int target) {
if (target == this.id) {
return this;
} else if (target > this.id) {
// 看右子樹是否為NULL,若為NULL就傳回NULL
if (this.right == null) {
return null;
} else {
// 不為NULL,就繼續從右子樹搜尋
return this.right.findTarget(target);
}
} else { // target < this.id
// 看左子樹是否為NULL,若為NULL就傳回NULL
if (this.left == null) {
return null;
} else {
// 不為NULL,就繼續從左子樹搜尋
return this.left.findTarget(target);
}
}
}
public Node findParent(int target) {
// 如果左子樹不是null,並且左子樹就是要找的目標,傳回目前節點,目前節點就是根節點
// 如果右子樹不是null,並且右子樹就是要找的目標,傳回目前節點,目前節點就是根節點
if ((this.left != null && this.left.id == target) ||
(this.right != null && this.right.id == target)) {
return this;
} else {
// 要找的目標,小於目前節點的id,代表要往左子樹找
if (target < this.id) {
// 如果左子樹是null,傳回NULL
if (this.left == null) {
return null;
} else {
// 往左子樹找目標
return this.left.findParent(target);
}
} else {
// 要找的目標大於等於目前節點,代表要往右子樹找
// 如果右子樹是NULL,傳回NULL
if (this.right == null) {
return null;
} else {
// 往右子樹找目標
return this.right.findParent(target);
}
}
}
}
@Override
public String toString() {
return "id=" + id ;
}
public void inOrder() {
if (this.left != null) {
this.left.inOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.inOrder();
}
}
public void add(Node node) {
if (node == null) return;
// 小於目前節點,新增在左子樹
if (node.id < this.id) {
// 左子樹是葉子節點,才新增
if (this.left == null) {
this.left = node;
} else { // 不是葉子,就繼續往左子樹找
this.left.add(node);
}
} else {
// 大於、等於目前節點,新增在右子樹
// 右子樹是葉子節點,才新增
if (this.right == null) {
this.right = node;
} else { // 不是葉子,就繼續往右子樹找
this.right.add(node);
}
}
}
}