河內塔
要把複雜的問題,切割成二部分,一個是最簡單的問題,也就是說不能再切割。
另一個部分就是,這個問題的處理方式適用於所有問題。
把以上二個問題的解決方式合併後,就可以解決第三個問題、第四個問題…。
河內塔要處理二個問題。
第一個是,只剩下一個盤子,如何處理這個問題?
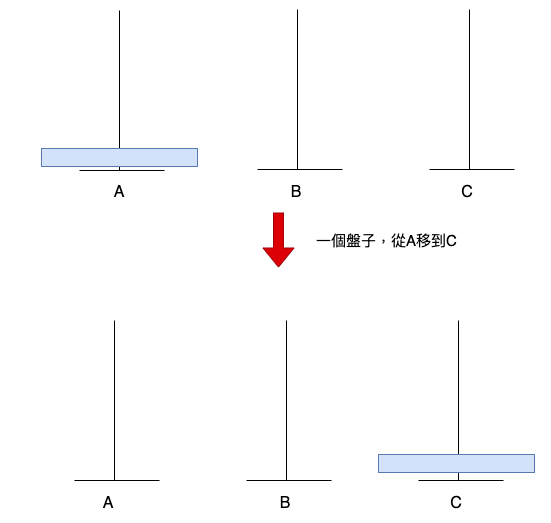
第二個是,若有兩個盤子,如何處理這個問題?處理兩個盤子,就可以處理三個盤子、四個盤子,因為都是相同的步驟。
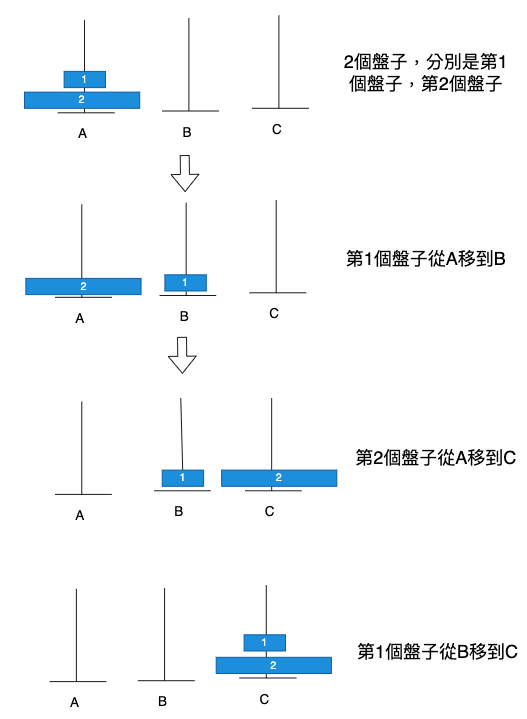
把2換成N,把1換成N-1。
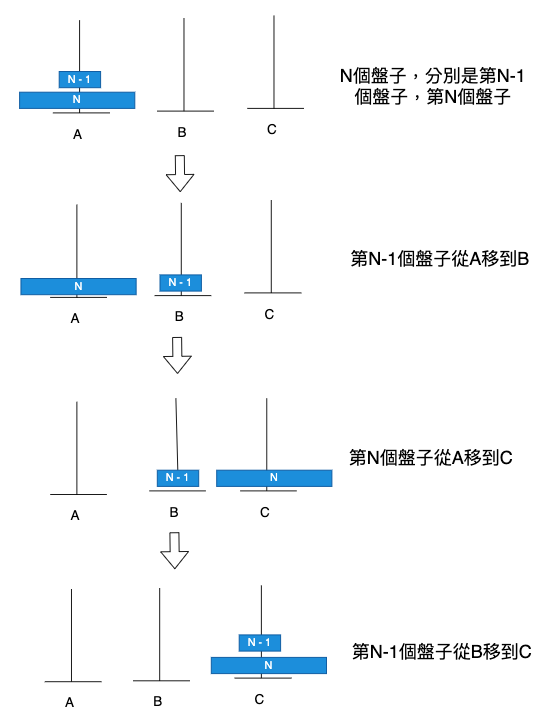
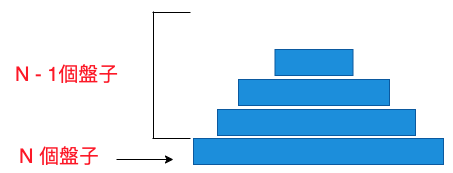
問題就只有以上二個解決方式,其它第N個盤子就想像成二個盤子,分別是第N個盤子與N-1個盤子。
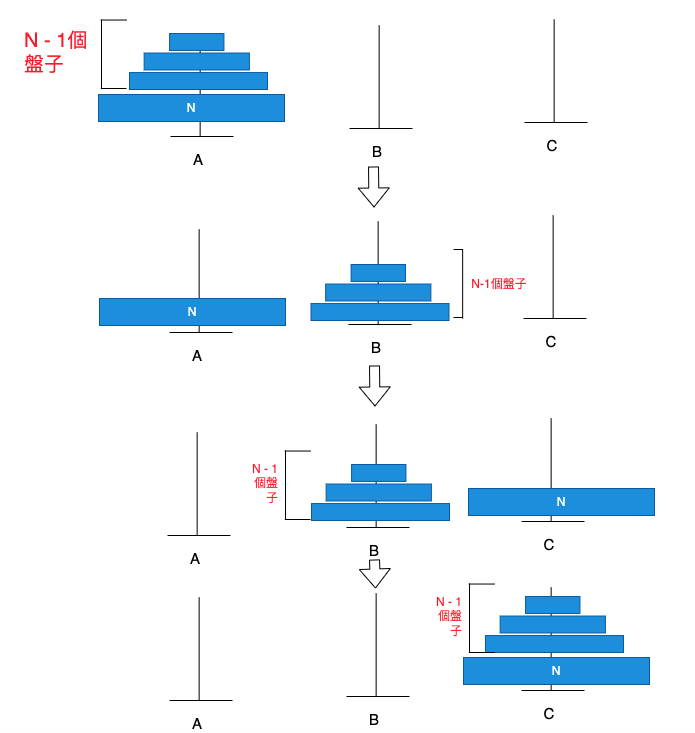
- 先把N-1個盤子從A移到B
- 再把N個盤子從A移到C
- 再把N-1個盤子從B移到C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class hanoi {
public static void main(String[] args) {
// 2 個盤子,有A B C 三個柱子
hanoiTower(2, 'A', 'B', 'C');
}
// 參數1: 幾個盤子
// 參數2: 從那開始移動
// 參數3: 輔助移動的柱子
// 參數4: 目的地
public static void hanoiTower(int n, char a, char b, char c) {
// 只有一個盤子,從A移到C
if (n == 1) {
System.out.println("n = 1 " + a + " -> " + c);
return;
}
// 有2個盤子,分別為n個盤子與n-1個盤子。
// 先把N-1個盤子從A移到B
hanoiTower(n - 1, a, c, b);
// 再把N個盤子從A移到C
System.out.println("n =" + n + " " + a + " -> " + c);
// 再把N-1個盤子從B移到C
hanoiTower(n - 1, b, a, c);
}
}