Prim
理論
Prim是尋找從某頂點出發,到全部頂點的最短路徑。
最短路徑(邊)的數量是頂點的數量 - 1,才能是到達各頂點之間的最少路徑(邊)。
3個頂點最少連接的邊是2條。(頂點數量3 - 1 = 最少連接的邊數2)
4個頂點最少連接的邊是3條。(頂點數量4 - 1 = 最少連接的邊數3)
從一個圖中,找出最少的邊數,但可以連接所有頂點。
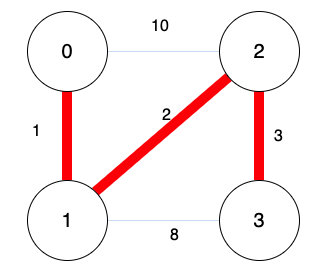
樹,是沒有迴路的,上圖中的紅色的線連接所有頂點,可以把它看成一棵樹。
要在圖Graph中找一棵樹,這一棵樹中文是最小成本展開樹Minimum Cost Spanning Tree,縮寫為MST,可以想像為要在圖中找最短路徑可以連接到各個頂點的樹,最短路徑也就是最小的成本。
Prim著重在頂點,由某個頂點出發,檢查此頂點出發的邊,那個最小。
找出最短路徑的邊與頂點
找出最短路徑的邊,尋找次數為(頂點的數量 - 1)。
第1次
把頂點0加入到訪問清單,從頂點0出發,有2條路,那一條更短?
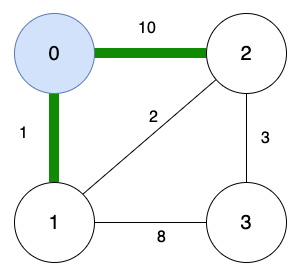
頂點0 到 頂點1的路更短,把「頂點1」加入訪問清單。
頂點0已經在訪問清單中了,所以不再加入。
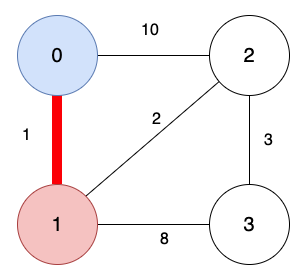
第2次
訪問清單目前有頂點0與頂點1。
頂點0:尋找跟頂點0連著的邊誰最短,排除掉已訪問過的邊。
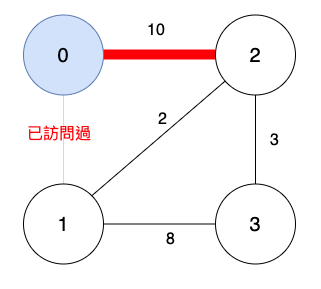
頂點1:尋找跟頂點1連著的邊誰最短,排除掉已訪問過的邊。
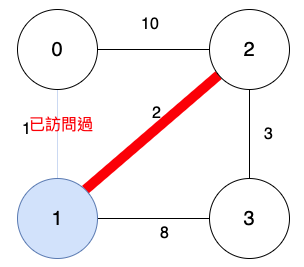
以上結果,誰的邊最短?

頂點1 到 頂點2的路更短,最短路徑相連的「頂點2」,加入訪問清單。
頂點1已經在訪問清單中了,所以不再加入。
第3次
訪問清單目前有頂點0與頂點1與頂點2。
頂點0:尋找跟頂點0連著的邊誰最短,排除掉已訪問過的邊。

頂點1:尋找跟頂點1連著的邊誰最短,排除掉已訪問過的邊。
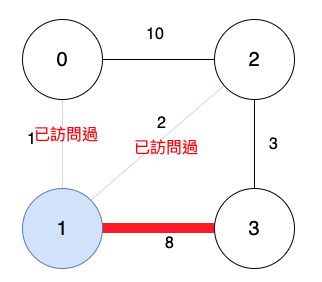
頂點2:尋找跟頂點2連著的邊誰最短,排除掉已訪問過的邊。
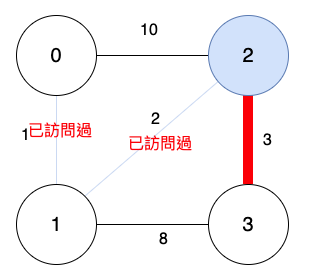
以上結果,誰的邊最短?

頂點2 到 頂點3的路更短,最短路徑相連的「頂點3」,加入訪問清單。
頂點2已經在訪問清單中了,所以不再加入。
準備工作
Prim演算法,要先把相鄰矩陣中,不能連接的邊全設為最大值MAX,包含自己連自己也要設為MAX。
1
2
3
4
5
matrix = new int[vertexLen][vertexLen];
matrix[0] = new int[]{MAX, 1, 10, MAX};
matrix[1] = new int[]{1, MAX, 2, 8};
matrix[2] = new int[]{10, 2, MAX, 3};
matrix[3] = new int[]{MAX, 8, 3, MAX};
visted陣列,記錄每一輪最短距離相連的頂點。
| 頂點 | 0 | 1 | 2 | 3 |
| visted | F | F | F | F |
程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
public class Prim {
private int[][] matrix;
private int vertexLen = 4;
public static final int MAX = 10000;
// 訪問清單
private boolean[] visted;
public Prim() {
// 不能連接的邊全設為最大值MAX,包含自己連自己也要設為MAX
matrix = new int[vertexLen][vertexLen];
matrix[0] = new int[]{MAX, 1, 10, MAX};
matrix[1] = new int[]{1, MAX, 2, 8};
matrix[2] = new int[]{10, 2, MAX, 3};
matrix[3] = new int[]{MAX, 8, 3, MAX};
visted = new boolean[vertexLen];
}
public void findShortDist() {
// 把頂點0加入訪問清單
visted[0] = true;
// 儲存最短路徑,也就最短的邊
List<int[]> result = new ArrayList<>();
// 尋找最短路徑次數為頂點數量 - 1
for (int i = 0; i < vertexLen - 1; i++) {
findShortDistVertex(result);
}
// 印出最短路徑,也就是最短的邊
for (int[] arr : result) {
System.out.println(Arrays.toString(arr));
}
}
public void findShortDistVertex(List<int[]> result) {
// 把最小權重(距離)設為最大值MAX
int minWeight = MAX;
// 最短距離連接的頂點,預設-1
int x = -1;
// 最短距離連接的頂點,預設-1
int y = -1;
// 遍歷訪問清單(若為最短距離頂點,會被加入清單中)
for (int i = 0; i < visted.length; i++) {
// 頂點是否在清單中
if (visted[i]) {
// 相連的邊那一條最短,而且相連的頂點未被訪問過
for (int j = 0; j < vertexLen; j++) {
// matrix[i][j]不為 MAX,代表頂點i與頂點j是有相連
if (matrix[i][j] != MAX && !visted[j]) {
// 距離是否比最小距離小
if (matrix[i][j] < minWeight) {
// 替換成最小距離
minWeight = matrix[i][j];
// 記錄最小距離相連的頂點
x = i;
y = j;
}
}
}
}
}
System.out.println("x = " + x + ", y = " + y + ", weight = " + minWeight);
// 把最小距離的頂點y加入清單
// x頂點已在清單中,不用再加入
visted[y] = true;
// 儲存最短距離的邊
result.add(new int[]{x, y});
}
public static void main(String[] args) {
Prim prim = new Prim();
prim.findShortDist();
}
}
x = 0, y = 1, weight = 1
x = 1, y = 2, weight = 2
x = 2, y = 3, weight = 3
[0, 1]
[1, 2]
[2, 3]