Kruskal
Prerequisites:
請一定要了解union find,才能繼續往下閱讀。
尋找最小的邊
KrusKal是尋找從某頂點出發,到全部頂點的最短路徑。
著重在邊,KrusKal會把邊全部由小到大排序,先取出最小的邊,並判斷加入此邊會不會造成迴路,不造成迴路才加入邊。
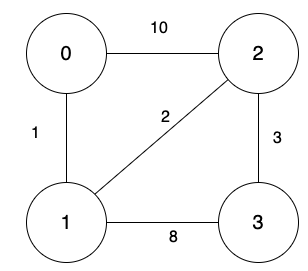
原本的圖。
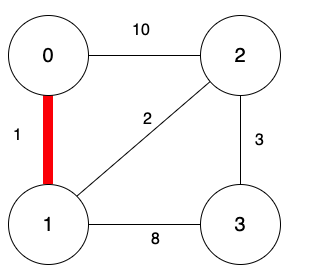
尋找圖中最小的邊。
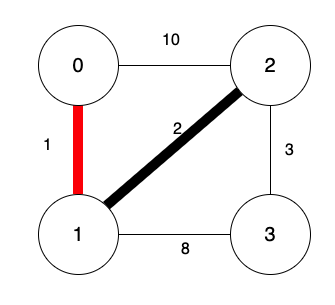
尋找圖中第2小的邊。
尋找圖中第3小的邊。
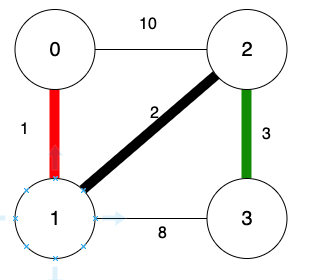
判斷迴路
假設頂點0到頂點2的距離為3,頂點2到頂點3的距離為3。
若選擇頂點0到頂點2,會造成迴路。
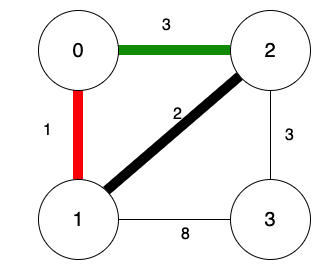
kruskal不允許有迴路,造成迴路的邊不選。
選擇頂點2到頂點3的距離為3。
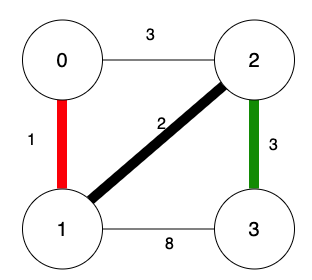
程式步驟
KrusKal的步驟如下:
- 把所有連接的邊,按照權值,由小到大排序。
- 檢查邊是否有迴路,沒有迴路就加入到list中。
- list記錄的是圖中每個頂點相連的最小路徑。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Krus {
private int[][] matrix ;
// 頂點數量
private int vertexLen = 4;
// 設最大值,MAX代表不能相連
public static final int MAX = 10000;
private int[] parent;
public Krus() {
matrix = new int[vertexLen][vertexLen];
// MAX代表不能相連,0代表自己連自己
matrix[0] = new int[]{0, 1, 10, MAX};
matrix[1] = new int[]{1, 0, 2, 8};
matrix[2] = new int[]{10, 2, 0, 3};
matrix[3] = new int[]{MAX, 8, 3, 0};
// 以下是union find演算法
parent = new int[vertexLen];
// 預設都爸爸都是自己
for (int i = 0; i < vertexLen; i++) {
parent[i] = i;
}
}
public EdgeData[] getEdges() {
int edgeNum = 0;
for (int i = 0; i < matrix.length; i++) {
// 此為無向圖,只看對角線0的右邊
// 無向圖,對角線0左邊與右邊都是對稱,只要看其中一邊就可以取出所有邊
for (int j = i + 1; j < matrix.length; j++) {
// MAX代表不是相連的
if (matrix[i][j] != MAX) {
// 計算邊的數量
edgeNum++;
}
}
}
// 建立邊的陣列
EdgeData[] edges = new EdgeData[edgeNum];
// 邊陣列的索引
int index = 0;
for (int i = 0; i < matrix.length; i++) {
// 只看對角線0的右邊。
for (int j = i + 1; j < matrix.length; j++) {
// MAX代表不是相連的
if (matrix[i][j] != MAX) {
// 建立邊
EdgeData edgeData = new EdgeData();
edgeData.setStart(i);
edgeData.setEnd(j);
edgeData.setWeight(matrix[i][j]);
// 把邊放入陣列
edges[index++] = edgeData;
}
}
}
return edges;
}
// 把邊按照權重,由小到大排序,採用氣泡排序
public void sort(EdgeData[] edges) {
for (int i = 0; i < edges.length; i++) {
for (int j = 0; j < edges.length - 1 - i; j++) {
if (edges[j].getWeight() > edges[j + 1].getWeight()) {
EdgeData temp = edges[j];
edges[j] = edges[j + 1];
edges[j + 1] = temp;
}
}
}
}
// 尋找頂點的祖父
public int find(int vertex) {
if (parent[vertex] == vertex) {
return vertex;
}
return find(parent[vertex]);
}
// 若二個頂點vertex1與vertex2的祖父不同
// 就能相連在一起
public void union(int vertex1, int vertex2) {
// 取出頂點1的祖先
int parent1 = find(vertex1);
// 取出頂點2的祖先
int parent2 = find(vertex2);
// 判斷是否為相同祖先
if (parent1 != parent2) {
// 若不同祖先,把祖先1的爸爸改為頂點2的祖先
parent[parent1] = parent2;
}
}
public static void main(String[] args) {
Krus krus = new Krus();
// 取得邊陣列
EdgeData[] edges = krus.getEdges();
// 排序邊
krus.sort(edges);
// 存放每個頂點相連的最短路徑
List<EdgeData> list = new ArrayList<>();
// 由小到大把最短路徑加入到list
for (int i = 0; i < edges.length; i++) {
int parent1 = krus.find(edges[i].getStart());
int parent2 = krus.find(edges[i].getEnd());
// 若2個頂點的祖先不同,不是同一個家族,才加入list中
// 不造成迴路,就能加入list
if (parent1 != parent2) {
krus.union(edges[i].getStart(), edges[i].getEnd());
list.add(edges[i]);
}
}
System.out.println("list = " + list);
}
}
// 邊的資料
class EdgeData {
// 連接頂點1
private int start;
// 連接頂點2
private int end;
// 權重(距離)
private int weight;
public int getStart() {
return start;
}
public void setStart(int start) {
this.start = start;
}
public int getEnd() {
return end;
}
public void setEnd(int end) {
this.end = end;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
@Override
public String toString() {
return "{" +
"s=" + start +
", e=" + end +
", w=" + weight +
'}';
}
}
list = [{s=0, e=1, w=1}, {s=1, e=2, w=2}, {s=2, e=3, w=3}]