Union Find
Union Find是一個尋找祖先(爸爸的爸爸的爸爸)演算法。
常常用來處理圖中是否有迴路。
簡易Union Find
先介紹簡易。
下面有三個頂點:
0, 1, 2
以下描述加入的過程:
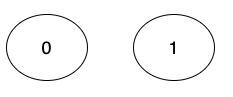
下圖中,0與1各自獨立。
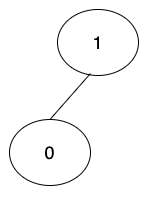
0 → 1 0與1相連,請想像成0的爸爸是1,也就是箭頭指向的是爸爸。
以下是記錄爸爸表格,預設都為-1,-1代表沒有爸爸,各自是獨立。
| 頂點 | 0 | 1 | 2 |
| parent | -1 | -1 | -1 |
0 → 1 0與1相連,0的爸爸是1,表格修改如下:
| 頂點 | 0 | 1 | 2 |
| parent | 1 | -1 | -1 |
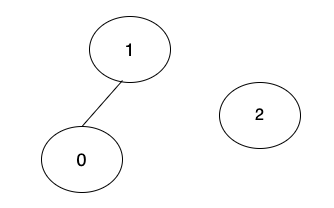
0 → 1 的樹,與2,各別獨立,沒有關係。
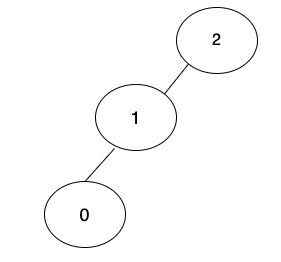
1 → 2 把1的爸爸指向2,修改parent表格。
| 頂點 | 0 | 1 | 2 |
| parent | 1 | 2 | -1 |
透過parent表格,可以從parent[0]找到爸爸是1,再從parent[1]找到爸爸是2,可以知道頂點0與1與2是同一個家族的,因為0的爸爸是1,1的爸爸是2。
以下參數為頂點vertex,若頂點沒有爸爸,是-1,就會傳回頂點本身。
若有爸爸,就會一路尋找爸爸的爸爸,直到已經是最頂的祖先(沒有爸爸,是-1),傳回最頂的祖先。
1
2
3
4
5
6
7
public int find(int vertex) {
while (parent[vertex] != -1) {
// 把爸爸傳給vertex,繼續找爸爸,直到-1找不到爸爸就離開迴圈。
vertex = parent[vertex];
}
return vertex;
}
2 → 0 若要把2的爸爸指向0,就會形成一個圈圈,也就是一個迴路,如下圖:
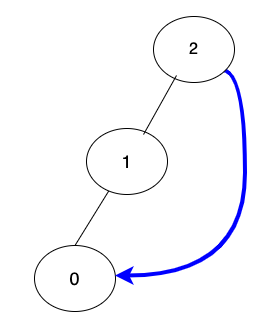
怎麼判斷是一個迴路呢?也就是頂點0的最頂的祖先是頂點2。而頂點2沒有爸爸,本身就是祖先,是樹的根節點,find(2)方法會傳回頂點自己,也就是2。
find(0) = 2
find(2) = 2
若頂點0與頂點2找到的祖先都是2,就是形成一個迴路,就不加入parent表格就不變更了。
union
接下來介紹,怎麼把二個樹合併。
假設目前表格與圖如下:
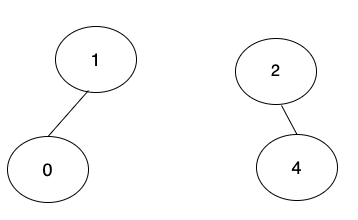
| 頂點 | 0 | 1 | 2 | 4 |
| parent | 1 | -1 | -1 | 2 |
- 頂點0的爸爸是1。
- 頂點4的爸爸是2。
二棵樹,分別為 0 → 1 與 4 → 2,箭頭指向的方向是爸爸,二棵樹各自獨立。
現在,要把合併二棵樹,0 - 4,0與4要相連在一起,二個家族要合併。
怎麼合併?怎麼把二邊的祖譜合在一起?
1.先找0的最頂的祖先,最頂的祖先為1。
2.再找4的最頂的祖先,最頂的祖先為2。
3.可以把0的祖先1指向2,如下圖:
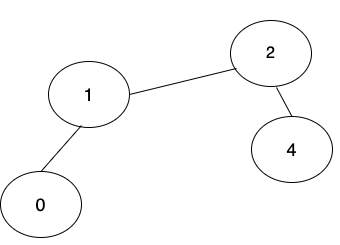
4.可以把4的祖先2指向1,如下圖:
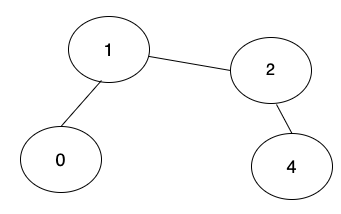
union程式碼
以下程式碼,參數為2個頂點,分別是頂點1(vertex1)與頂點2(vertex2)。
1
2
3
4
5
6
7
8
9
10
11
12
// vertex1 → vertex2,要把箭頭指向的vertex2設為爸爸
public void union(int vertex1, int vertex2) {
// vertex1的最頂祖先
int parent1 = find(vertex1);
// vertex2的最頂祖先
int parent2 = find(vertex2);
// 若不相同,不會形成迴路
if (parent1 != parent2) {
// 把vertex2的祖先設為爸爸
parent[parent1] = parent2;
}
}
完整程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class SimpleUniFind {
private int[] parent;
private int vertexNum = 4;
public static void main(String[] args) {
SimpleUniFind uniFind = new SimpleUniFind();
uniFind.union(0,1);
uniFind.union(1,2);
uniFind.union(2,0);
uniFind.print();
}
public SimpleUniFind() {
parent = new int[vertexNum];
Arrays.fill(parent,-1);
}
public int find(int vertex) {
while (parent[vertex] != -1) {
vertex = parent[vertex];
}
return vertex;
}
public void union(int vertex1, int vertex2) {
int parent1 = find(vertex1);
int parent2 = find(vertex2);
if (parent1 != parent2) {
parent[parent1] = parent2;
}
}
public void print() {
System.out.println(Arrays.toString(parent));
}
}
Union find
parent表格預設爸爸就是頂點自己。
| 頂點 | 0 | 1 | 2 |
| parent | 0 | 1 | 2 |
下面有三個頂點:
0, 1, 2
0 與 1各自獨立。

0 → 1 0與1相連,請想像成0的爸爸是1,也就是箭頭指向的是爸爸。

修改0的爸爸是1,預設爸爸都是頂點本身自己,若不是自己,就代表有爸爸。
| 頂點 | 0 | 1 | 2 |
| parent | 1 | 1 | 2 |
0 → 1 與 2各自獨立。

1 → 2 1的爸爸指向2,修改parent表格。

| 頂點 | 0 | 1 | 2 |
| parent | 1 | 2 | 2 |
透過parent表格,可以從parent[0]找到爸爸是1,再從parent[1]找到爸爸是2,可以知道頂點0與1與2是同一個家族的,因為0的爸爸是1,1的爸爸是2。
以下參數為頂點vertex,若頂點的爸爸是頂點本身,就不進入while迴圈,傳回頂點本身。
若有爸爸,就會一路尋找爸爸的爸爸,直到已經是最頂的祖先(爸爸是頂點本身,離開迴圈),傳回最頂的祖先。
1
2
3
4
5
6
7
8
9
public int find(int vertex) {
// 離開迴圈的條件:爸爸是頂點本身,離開迴圈
// 進入迴圈的條件:爸爸不是頂點本身
while (parent[vertex] != vertex) {
// 把爸爸傳給vertex,繼續找爸爸
vertex = parent[vertex];
}
return vertex;
}
另一種寫法是遞迴寫法,二者意思相同。
1
2
3
4
5
6
public int find(int vertex) {
if (parent[vertex] == vertex) {
return vertex;
}
return find(parent[vertex]);
}
完整程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class UniFind {
private int[] parent;
private int vertexNum = 4;
public static void main(String[] args) {
UniFind uniFind = new UniFind();
uniFind.union(0,1);
uniFind.union(1,2);
uniFind.union(2,0);
}
public UniFind() {
parent = new int[vertexNum];
for (int i = 0; i < vertexNum; i++) {
parent[i] = i;
}
}
public int find(int vertex) {
if (parent[vertex] == vertex) {
return vertex;
}
return find(parent[vertex]);
}
public void union(int vertex1, int vertex2) {
int parent1 = find(vertex1);
int parent2 = find(vertex2);
if (parent1 != parent2) {
parent[parent1] = parent2;
}
}
}
關於爸爸
之前頂點1 → 頂點2,都把頂點2的祖先設為爸爸,但也可以相反。
頂點1 → 頂點2,把頂點1的祖先設為爸爸,結果都會是相同的。
1
2
3
4
5
6
7
public void union(int vertex1, int vertex2) {
int parent1 = find(vertex1);
int parent2 = find(vertex2);
if (parent1 != parent2) {
parent[parent2] = parent1;
}
}