Floyd
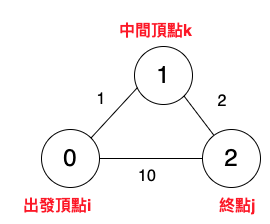
比較出發頂點i → 終點j的距離，與出發頂點i → 中間頂點k → 終點j的距離，誰比較短？
下圖中，出發頂點0 → 終點2的距離為10，出發頂點0 → 中間頂點1 → 終點2的距離為3，很明顯0 → 1 → 2的距離更短。
row列是i，column欄是j。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | 0 | 0 | 0 |
| i=1 | 1 | 1 | 1 |
| i=2 | 2 | 2 | 2 |
出發頂點i為0，終點j為1。
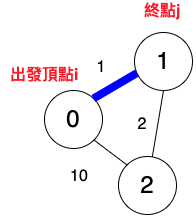
終點j為1的前一個為頂點0。
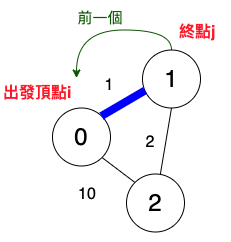
出發頂點i為0，終點j為2。
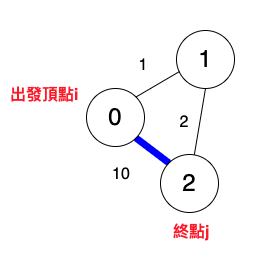
終點j為2的前一個為頂點0。
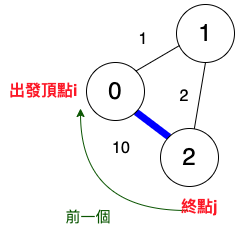
從上面的解釋可以知道，預設路徑表中，終點為j，它的前一個頂點預設為出發點i，預設i為前一個頂點。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | 0 | 0 | 0 |
| i=1 | 1 | 1 | 1 |
| i=2 | 2 | 2 | 2 |
matrix表格
matrix表格是記錄各個頂點間距離，如下:
| j=0 | j=1 | j=2 | |
| i=0 | 0 | 1 | 10 |
| i=1 | 1 | 0 | 2 |
| i=2 | 10 | 2 | 0 |
其中，對角線為0，代表0 → 0，頂點0到頂點0，是0距離。
1 → 1，頂點1到頂點1，是0距離。
2 → 2，頂點2到頂點2，是0距離。
preVertex表格
preVertex表格記錄終點j的前一個頂點。
出發頂點i → 終點j，比出發頂點i → 中間頂點k → 終點j，距離更長。
出發頂點i → 中間頂點k → 終點j，距離更短的話，要記錄終點j的前一個頂點是誰。
若是出發頂點i → 終點j距離更短，終點j的前一個為出發頂點。
若出發頂點i → 中間頂點k → 終點j，距離更短，終點j的前一個頂點為中間頂點k。
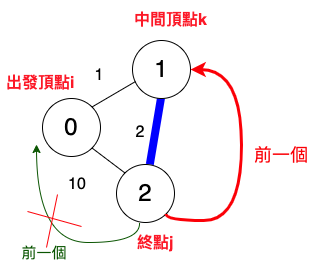
預設終點j的前一個頂點是出發頂點i。
以下是記錄出發頂點i → 終點j，終點j的前一個頂點是誰。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | 0 | 0 | 0 |
| i=1 | 1 | 1 | 1 |
| i=2 | 2 | 2 | 2 |
現在要找中間頂點k → 終點j，終點j的前一個頂點是誰。
所以把表格重新定義如下:
| 中間頂點\終點 | j=0 | j=1 | j=2 |
| k=0 | 0 | 0 | 0 |
| k=1 | 1 | 1 | 1 |
| k=2 | 2 | 2 | 2 |
下圖中，中間頂點k為1 → 終點j為2，對映上表(k=1,j=2)，(1,2) = 1，終點j的前一個頂點是1。
接著把中間頂點k → 終點j的前一個頂點，存到preVetex表格(i,j)位置，記錄出發頂點i → 終點j，終點j的前一個頂點是1。
推導路徑的時候，就可以pretex(i,j)找到終點j的前一個頂點是誰。
中間頂點k為0
當出發頂點i是0，當中間頂點k是0，對映j=0,1,2。
出發頂點i → 中間頂點k → j終點
0→0→0，與0→0→1，與0→0→2，我都視為0→0，0→1，0→2，沒有變化。
當出發頂點i是1，當中間頂點k是0，對映j=0,1,2
1→0→0
1→0→0，分解成2種路徑，分別是1→0(i=1,j=0)，與0→0(i=0,j=0)，i是出發頂點，j是終點，查下表。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | 0 | 1 | 10 |
| i=1 | 1 | 0 | 2 |
| i=2 | 10 | 2 | 0 |
1→0，距離為1。
0→0，距離為0。
仍是沒有比1→0的距離1短，不更新matrix表格與preVertex表格。
1→0→1
1→0→1，分解成2種路徑，分別是1→0(i=1,j=0)，與0→1(i=0,j=1)，i是出發頂點，j是終點，查下表。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | 0 | 1 | 10 |
| i=1 | 1 | 0 | 2 |
| i=2 | 10 | 2 | 0 |
1→0，距離為1。
0→1，距離為1。
1→0→1 = 相加距離為2，仍是沒有比1→1的距離0短，不更新matrix表格與preVertex表格。
1→0→2
1→0→2，分解成2種路徑，分別是1→0(i=1,j=0)，與0→2(i=0,j=2)，i是出發頂點，j是終點，查下表。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | 0 | 1 | 10 |
| i=1 | 1 | 0 | 2 |
| i=2 | 10 | 2 | 0 |
1→0，距離為1。
0→2，距離為10。
1→0→2 = 相加距離為11，仍是沒有比1→2的距離2短，不更新matrix表格與preVertex表格。
中間頂點k為1
當出發頂點i是0，當中間頂點k是1，對映j=0,1,2。
出發頂點i → 中間頂點k → j終點
0→1→0，與0→1→1，與0→1→2，有二個頂點相同的，等同於0→1，等於沒有中間頂點，而是從頂點0直達頂點1，跟沒有透過中間頂點的結果是一樣，距離不會更小，所以我只注重在3個頂點不同。
0→1→2
0→1→2，分解成2種路徑，分別是0→1(i=0,j=1)，與1→2(i=1,j=2)，i是出發頂點，j是終點，查下表。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | 0 | 1 | 10 |
| i=1 | 1 | 0 | 2 |
| i=2 | 10 | 2 | 0 |
0→1，距離為1。
1→2，距離為2。
0→1→2 = 1 + 2 相加距離為3，比0→2的距離10更短，更新matrix表格與preVertex表格。
更新matrix表格
| matrix | j=0 | j=1 | j=2 |
| i=0 | 0 | 1 | 3 |
| i=1 | 1 | 0 | 2 |
| i=2 | 10 | 2 | 0 |
更新preVertex表格
preVertex是記錄每一個終點j的前一個頂點是誰？若是直達的話，預設是出發頂點i。
preVertex的更新，只在乎「中間頂點k」到「終點j」，終點j的「前一個頂點」是誰？根據下表找出(k=1,j=2)，[1,2] = 1，1是終點j的前一個頂點。
| 中間\終點 | j=0 | j=1 | j=2 |
| k=0 | 0 | 0 | 0 |
| k=1 | 1 | 1 | 1 |
| k=2 | 2 | 2 | 2 |
接著把出發頂點i → 終點j的「前一個頂點」，更新成k中間頂點 → j終點, 終點j的「前一個頂點」，剛才找到的結果為1，是終點j前一個頂點。
(i=0,j=2)，更新為1，也就是從0 → 2，終點2的前一個頂點是1，而不是原來的0，因為從0→1→2，距離為3，從中間頂點1到終點2，終點2的前一個頂點是1，距離會更短。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | 0 | 0 | |
| i=1 | 1 | 1 | 1 |
| i=2 | 2 | 2 | 2 |
要如何從以上路徑表推導路徑？若出發頂點i → 終點j的路徑表為i，代表沒有中間頂點k，i → j已經是最短路徑。
若有中間頂點k，如上表，出發頂點i為0 → 終點j為2，終點j為2的前一個頂點是1，而不是頂點0。
拿到中間頂點k，查出發頂點i為0 → 中間頂點k為1(i=0,k=1)，若(0,1) == 出發頂點i，就代表找到出發頂點，停止搜尋路徑。
| j=0 | j=1 | j=2 | |
| i=0 | 0 | 0 | 1 |
| i=1 | 1 | 1 | 1 |
| i=2 | 2 | 2 | 2 |
程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
public class Floyed {
private int[][] matrix;
private int[][] preVertex;
private int vertexLen = 3;
public Floyed() {
matrix = new int[vertexLen][vertexLen];
matrix[0] = new int[]{0, 1, 10};
matrix[1] = new int[]{1, 0, 2};
matrix[2] = new int[]{10, 2, 0};
// preVertex尋找前一個頂點，i是出發頂點，j是終點
preVertex = new int[vertexLen][vertexLen];
for (int i = 0; i < preVertex.length; i++) {
// 預設前一個頂點是i出發頂點，若沒有中間頂點
// i → j，是直達，j頂點的前一個頂點是i
Arrays.fill(preVertex[i], i);
}
}
public void floyed() {
int len = 0;
for (int k = 0; k < vertexLen; k++) {
for (int i = 0; i < vertexLen; i++) {
for (int j = 0; j < vertexLen; j++) {
len = matrix[i][k] + matrix[k][j];
if (len < matrix[i][j]) {
matrix[i][j] = len;
preVertex[i][j] = preVertex[k][j];
}
}
}
}
}
public void print() {
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
System.out.print(matrix[i][j] + ", ");
}
System.out.println();
}
System.out.println();
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
System.out.print(preVertex[i][j] + ", ");
}
System.out.println();
}
}
// 參數出發頂點i,終點j
// 印出的結果是呈現倒敘的方式，根據箭頭的方法來看路徑
public void printPath(int i, int j) {
// 終點
System.out.print(j);
// 出發頂點i → 終點j，前一個頂點是誰？
int pre = preVertex[i][j];
// 若前一個頂點是出發頂點i，就代表沒有中間頂點k。
// 若前一個頂點「不是」出發頂點i，就代表有中間頂點，繼續找，直到前一個頂點為i(出發頂點)。
while (pre != i) {
System.out.print("<-" + pre);
// 繼續找前一個頂點，i是出發頂點是固定
// 直到前一個頂點是i，pre == i，就離開迴圈
pre = preVertex[i][pre];
}
// 出發頂點
System.out.print("<-" + i);
}
public static void main(String[] args) {
Floyed floy = new Floyed();
floy.floyed();
floy.print();
// 找頂點2 → 頂點0之間的路徑
floy.printPath(2,0);
}
}
0, 1, 3,
1, 0, 2,
3, 2, 0,
0, 0, 1,
1, 1, 1,
1, 2, 2,
0<-1<-2
另一種路徑表程式碼
預設路徑表preVertex全為-1，-1代表沒有中間頂點。
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | -1 | -1 | -1 |
| i=1 | -1 | -1 | -1 |
| i=2 | -1 | -1 | -1 |
若出發頂點i → 終點j，有中間頂點k，直接存入preVertex(i, j)的位置。
preVertex[i][j] = k;
| 出發\終點 | j=0 | j=1 | j=2 |
| i=0 | -1 | -1 | 1 |
| i=1 | -1 | -1 | -1 |
| i=2 | 1 | -1 | -1 |
印出路徑要拆分二部分遞迴，分別為:
- 出發頂點i → 中間頂點k
- 中間頂點k → 終點j
遞迴結束條件為，preVertex[i][j] == -1，代表沒有中間節點了，把路徑i與路徑j印出來。
尋找出發頂點i為0 → 終點j為2，透過上面表格preVertex[0][2] = 1，找出中間頂點k為1。
拆分成二部分如下:
- 出發頂點i為0 → 中間頂點k為1，
preVertex[0][1] = -1，印出0->1 - 中間頂點k為1 → 終點j為2，
preVertex[1][2] = -1，印出1->2
1
2
3
4
5
6
7
8
9
public void printPath(int i, int j) {
if (preVertex[i][j] == -1) {
System.out.println(i + "->" + j);
return;
}
int k = preVertex[i][j];
printPath(i,k);
printPath(k,j);
}
完整程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
public class Floyed {
private int[][] matrix;
private int[][] preVertex;
private int vertexLen = 3;
public Floyed() {
matrix = new int[vertexLen][vertexLen];
matrix[0] = new int[]{0, 1, 10};
matrix[1] = new int[]{1, 0, 2};
matrix[2] = new int[]{10, 2, 0};
preVertex = new int[vertexLen][vertexLen];
for (int i = 0; i < preVertex.length; i++) {
Arrays.fill(preVertex[i], -1);
}
}
public void floyed() {
int len = 0;
for (int k = 0; k < vertexLen; k++) {
for (int i = 0; i < vertexLen; i++) {
for (int j = 0; j < vertexLen; j++) {
len = matrix[i][k] + matrix[k][j];
if (len < matrix[i][j]) {
matrix[i][j] = len;
preVertex[i][j] = k;
}
}
}
}
}
public void print() {
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
System.out.print(matrix[i][j] + ", ");
}
System.out.println();
}
System.out.println();
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
System.out.print(preVertex[i][j] + ", ");
}
System.out.println();
}
}
public void printPath(int i, int j) {
if (preVertex[i][j] == -1) {
System.out.println(i + "->" + j);
return;
}
int k = preVertex[i][j];
printPath(i,k);
printPath(k,j);
}
public static void main(String[] args) {
Floyed floy = new Floyed();
floy.floyed();
floy.print();
floy.printPath(0,2);
}
}
-1, -1, 1,
-1, -1, -1,
1, -1, -1,
0->1
1->2