N皇后
以下有4*4的棋盤。
一列(row),只能放一個皇后,同一欄(column),不能放皇后,左斜角,右斜角也不能放皇后。
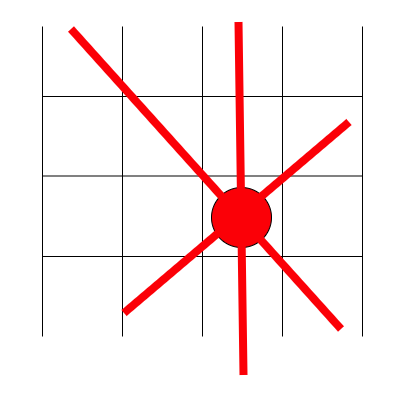
之後的程式中,i代表列row,j代表欄column,以(i,j)表示,代替座標(x,y)。
放置皇后過程
第0列,i=0,先嘗試在(0,0)的位置放第一個皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
第1列,i=1,由於(0,0)同一欄、左斜、右斜,都不能放皇后,所以在(1,2)的位置放第一個皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
第2列,i=2,由於(0,0)與(1,2)同一欄、左斜、右斜,都不能放皇后,所以返回上一列i=1。
x代表4個位置都無法放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | x | x | x | x |
| i=3 |
返回第1列,i=1,由於i=1的皇后位置,導致後面完全無法放皇后,把皇后位置撤銷。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
第1列,i=1,嘗試(1,3)放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
第2列,i=2,經過同一欄、左斜、右斜的檢驗後,可把皇后放在(2,1)。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 |
第3列,i=3,由於同一欄、左斜、右斜,都不能放皇后,所以返回上一列i=2。
x代表4個位置都無法放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 | x | x | x | x |
返回第2列,i=2,由於i=2的皇后位置,導致後面完全無法放皇后,把皇后位置撤銷,經過檢測,已無其它位置可以放皇后,返回第1列。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
返回第1列,i=1,由於i=1的皇后位置,導致後面完全無法放皇后,把皇后位置撤銷,經過檢測,已無其它位置可以放皇后,返回第0列。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
返回第0列,i=0,由於i=0的皇后位置,導致後面完全無法放皇后,把皇后位置撤銷。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | ||||
| i=1 | ||||
| i=2 | ||||
| i=3 |
第0列,i=0,嘗試在(0,1)放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
第1列,i=1,經過檢測,在(1,3)放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
第2列,i=2,經過檢測,在(2,0)放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 |
第3列,i=3,經過檢測,在(3,2)放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 | Q |
這是其中一個放皇后的方法,以下是另一個皇后放法。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 | Q |
程式碼顯示結果
以點.代表空格,以Q代表皇后
.Q..
...Q
Q...
..Q.
程式碼初始化
先準備棋盤的初始化。
1
2
3
4
5
6
7
8
9
10
11
12
// 準備棋盤
private char[][] board;
// 4乘4大小的棋盤
private int N = 4;
public Queen() {
// 建立棋盤
board = new char[N][N];
// 預設字元陣列都是點.
for (int i = 0; i < board.length; i++) {
Arrays.fill(board[i],'.');
}
}
檢查條件
同一欄(column),往上左斜角,往上右斜角也不能放皇后。
由於遞迴只會造成上面的列數要檢查,所以不考慮下面的列,所以只檢查往上左斜與往上右斜。
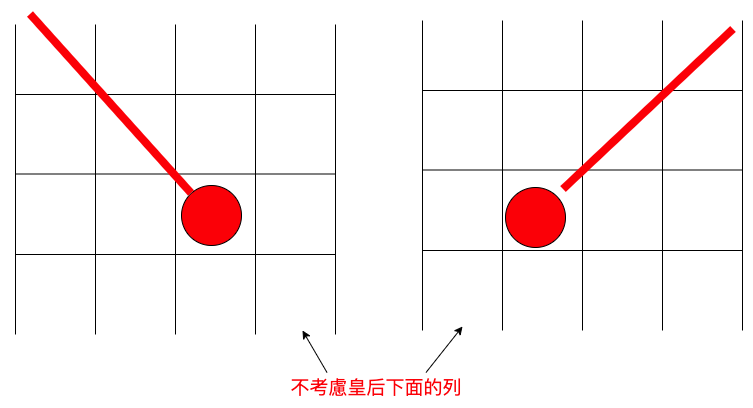
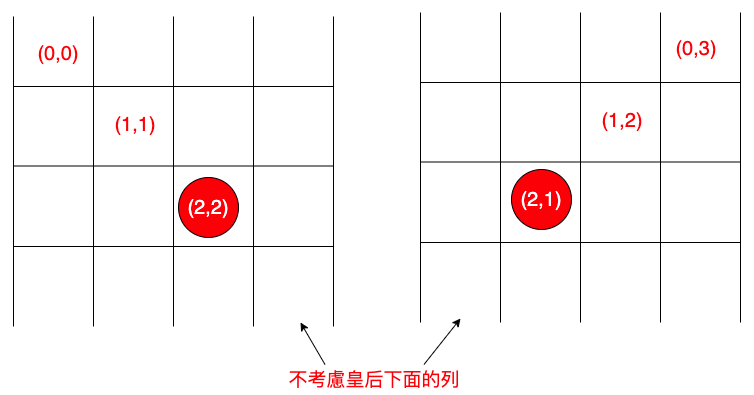
(i,j)持續往左上移動,要確保在棋盤範圍之內,二者要大於0。
(i,j)持續往右上移動,要確保在棋盤範圍之內,i要大於0,j要小於棋盤邊界大小。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 參數 列row與欄column,檢查是否能放皇后
public boolean isValidate(int row, int col) {
// 檢查每一列row,在同一欄是否有皇后
for (int i = 0; i <= row; i++) {
if (board[i][col] == 'Q') {
return false;
}
}
// i與j的初始值是(row - 1, col - 1),假設(row=3,col=3)
// 就會變成(2,2),也就是上面左斜,持續減1
// (3,3) -> (2,2) -> (1,1) -> (0,0)
// 由於遞迴只會造成上面的列數要檢查,所以不考慮下面的列
// 不能減到超出棋盤邊界,不能為-1
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') {
return false;
}
}
// i與j的初始值是(row - 1, col + 1),假設(row=3,col=0)
// 就會變成(2,1),也就是上面右斜,持續往上右斜檢查
// (3,0) -> (2,1) -> (1,2)
// 由於遞迴只會造成上面的列數要檢查,所以不考慮下面的列
// 不能減到超出棋盤邊界,不能為-1,也不能col + 1,加到超出board.length
for (int i = row - 1, j = col + 1; i >=0 && j < board.length; i--, j++) {
if (board[i][j] == 'Q') {
return false;
}
}
return true;
}
dfs程式碼
dfs方法,參數i為列row,第x列放置皇后,一開始會dfs(0)第0列開始放皇后。註解有說明程式運作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 參數 i為列row,針對每一列row,放皇后
public void dfs(int i, List<List<String>> result) {
// 如果 i == 4,代表上一次遞迴是dfs(3)
// dfs(3) row=3 i=3,代表第3列的皇后成功放置了,才會呼叫dfs(4)
// 注意!不是i == board.length - 1,沒有減1
// 把第0-3列的所有皇后放法存在List中,並離開遞迴,返回dfs(3)
if (i == board.length) {
List<String> list = new ArrayList<String>();
for (char[] row: board) {
// 把字串陣列轉成String存到List中
list.add(new String(row)) ;
}
result.add(list);
return; // 返回dfs(3)
}
// j代表column,對每一欄嘗試放置皇后
for (int j = 0; j < board[0].length; j++) {
// 檢查欄 左斜 右斜 是否有放其它皇后
if (isValidate(i, j)) {
// 放皇后
board[i][j] = 'Q';
// dfs(下一列row) 下一列放皇后
dfs(i + 1, result);
// 找到皇后放置的方法,dfs(4)會回到此處dfs(3),清空皇后
// 一路返回dfs(2) -> 清空皇后 -> dfs(1) -> 清空皇后 -> dfs(0) -> 清空皇后
// 清空皇后後,再尋找新的放置皇后的路徑。
// 撤銷皇后也會回到此處
board[i][j] = '.';
}
}
}
Debug
以下是程式碼Debug的過程,以及如何把皇后撤銷,與找到皇后路徑,重點在於撤銷皇后的過程,這是backtracking的技巧。
1.dfs(0) 第0列 row = 0 ,把board[0][0]放一個Q,Q代表Queen皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
2.board[0][0]=Q
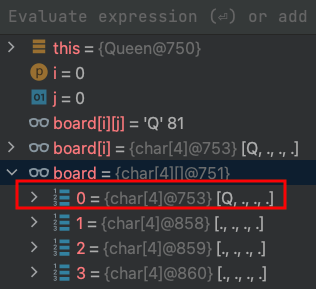
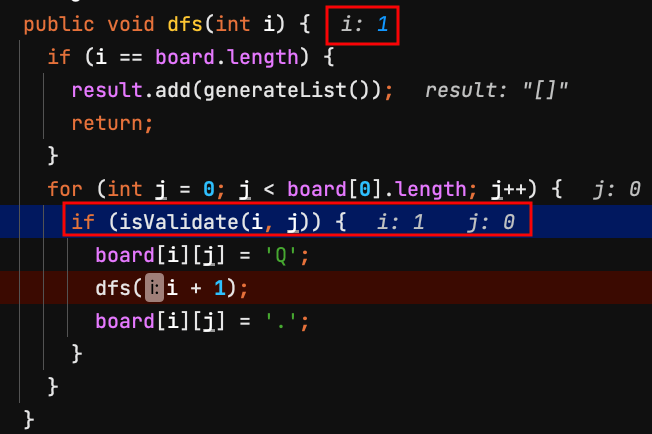
3.dfs(1) 第1列 row = 1,檢查board[1][0]是否能放皇后?不能,j換下一個。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
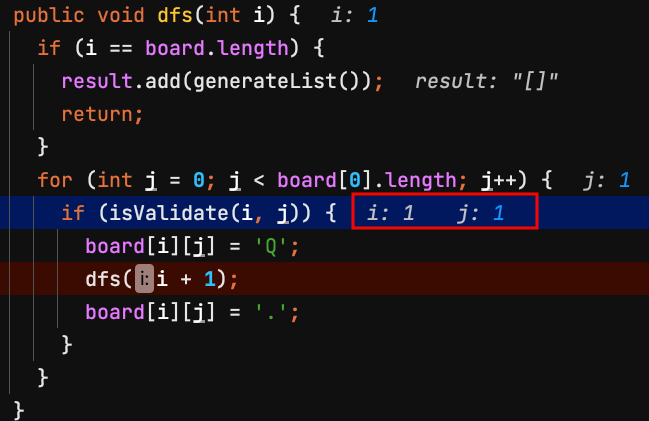
4.dfs(1) 第1列 row = 1,檢查board[1][1]是否能放皇后?不能,j換下一個。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
5.dfs(1) 第1列 row = 1,檢查board[1][2]是否能放皇后?
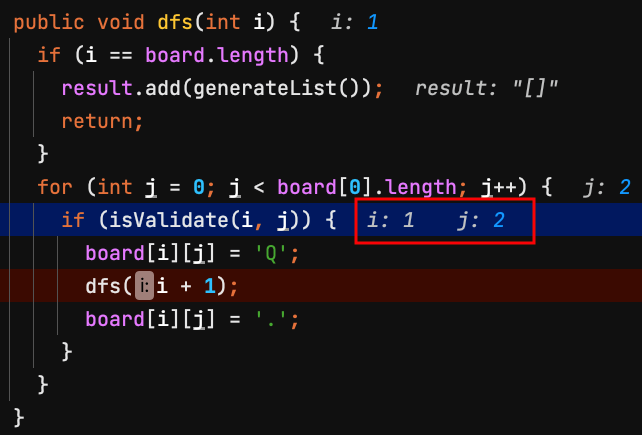
6.可以放皇后,下一列dfs(2)
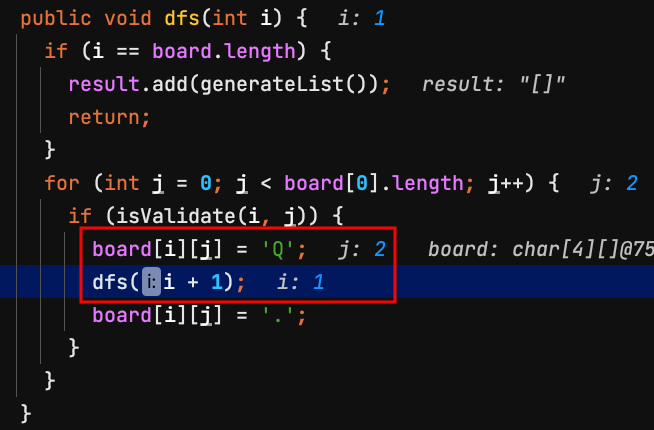
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
7.board[1][2]=Q
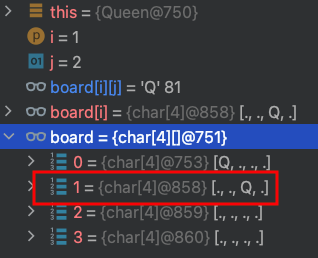
8.dfs(2) 第2列 row = 2,檢查board[2][0]是否能放皇后?不能,j換下一個。
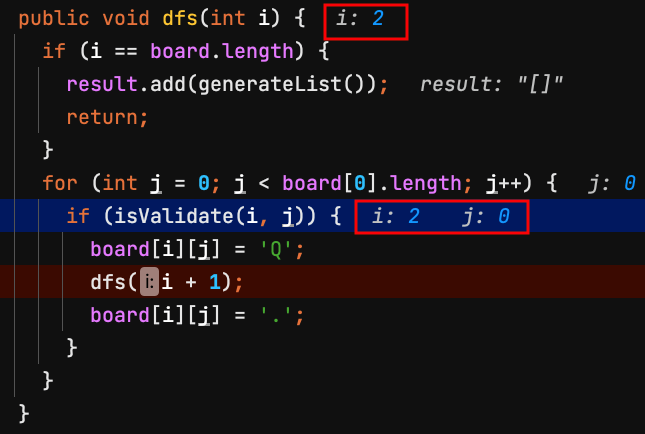
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
9.dfs(2) 第2列 row = 2,檢查board[2][1]是否能放皇后?不能,j換下一個。
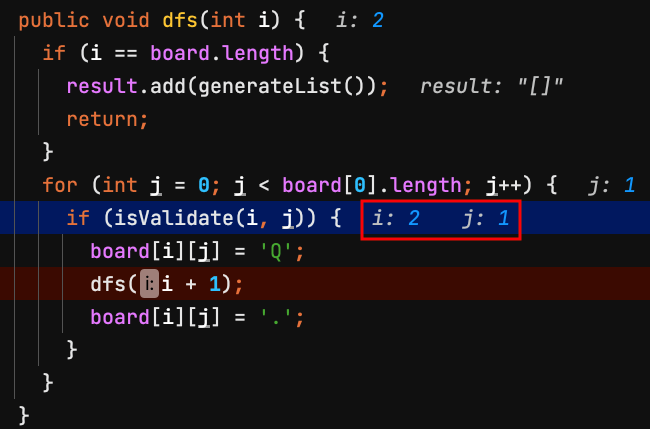
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
10.dfs(2) 第2列 row = 2,檢查board[2][2]是否能放皇后?不能,j換下一個。
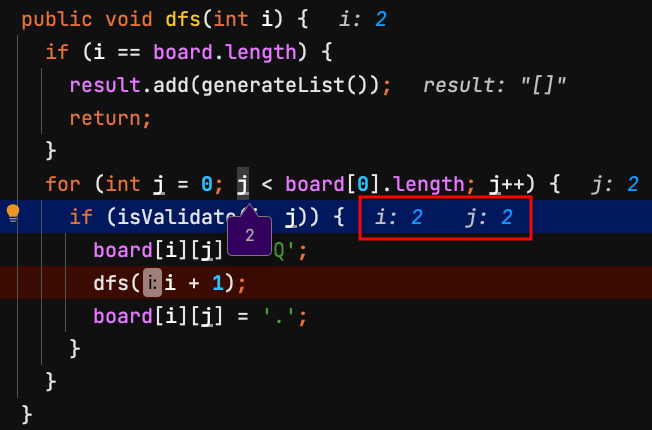
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
11.dfs(2) 第2列 row = 2,檢查board[2][3]是否能放皇后?不能,離開dfs(2)方法。
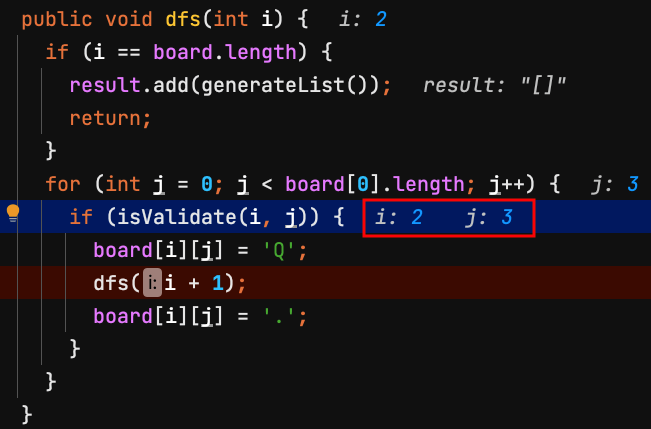
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
12.離開dfs(2),回到上一個dfs(1)方法,把第1列board[1][2]皇后移掉,變成預設值.。
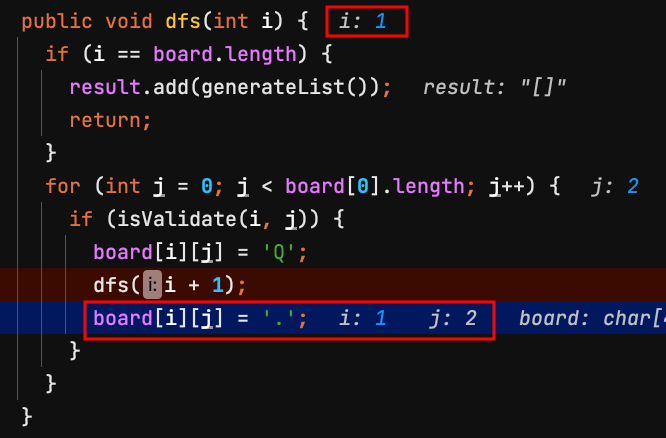
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
13.board[1][2]= .
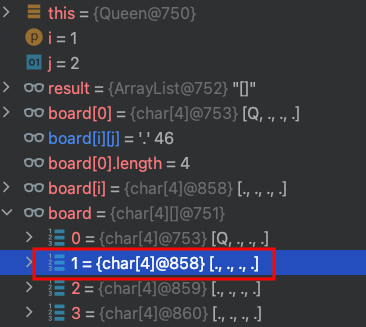
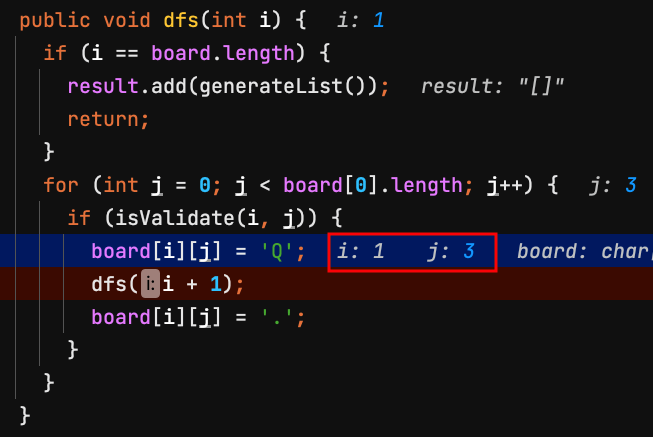
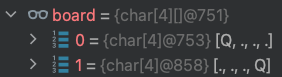
14.dfs(1) 第1列 row = 1,經過檢查board[1][3]可以放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
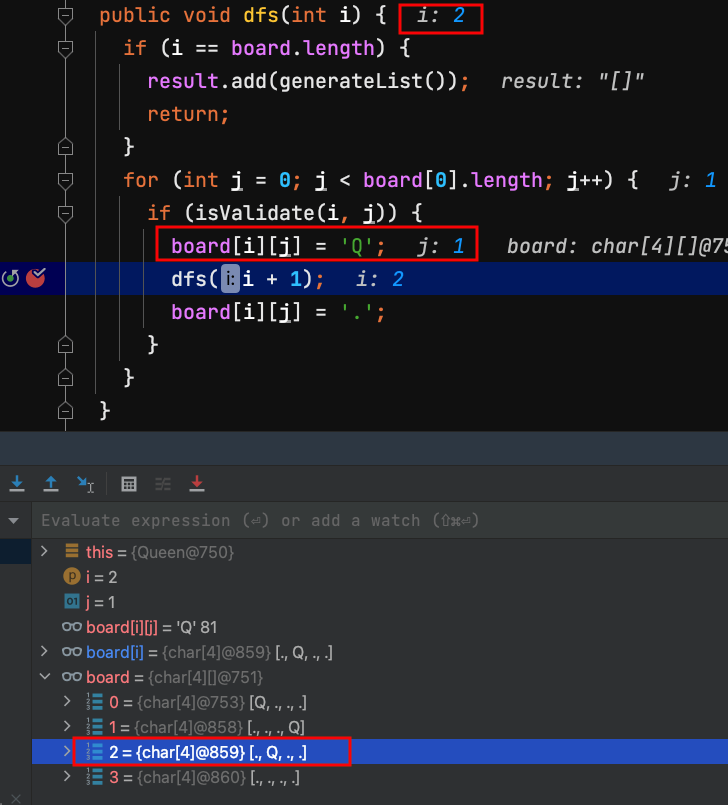
15.中間略過一些步驟,dfs(2) 第2列 row = 2,經過檢查board[2][1]可以放皇后。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 |
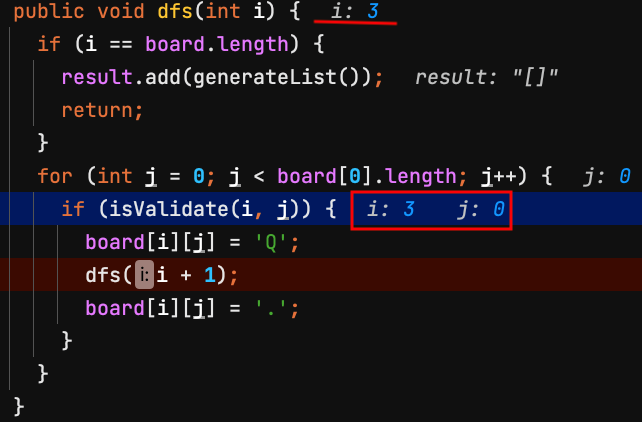
16.dfs(3) 第3列 row = 3,檢查board[3][0]是否能放皇后?不能,j換下一個。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 |
17.dfs(3) 第3列 row = 3,檢查board[3][1]是否能放皇后?不能,j換下一個。
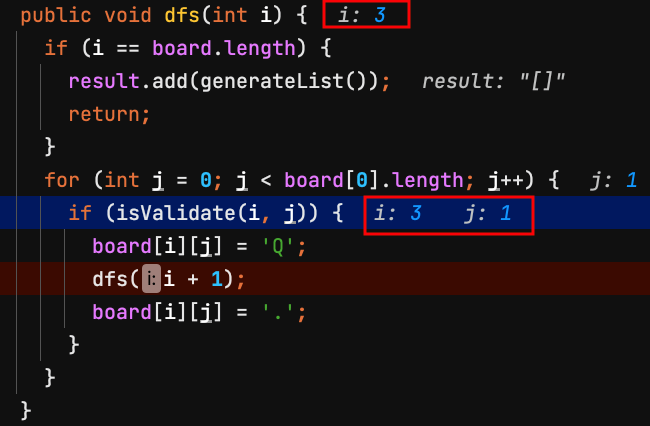
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 |
18.dfs(3) 第3列 row = 3,檢查board[3][2]是否能放皇后?不能,j換下一個。
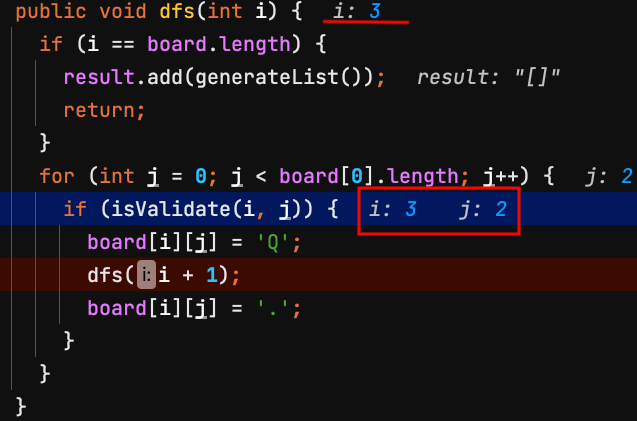
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 |
19.dfs(3) 第3列 row = 3,檢查board[3][3]是否能放皇后?不能,離開dfs(3)。
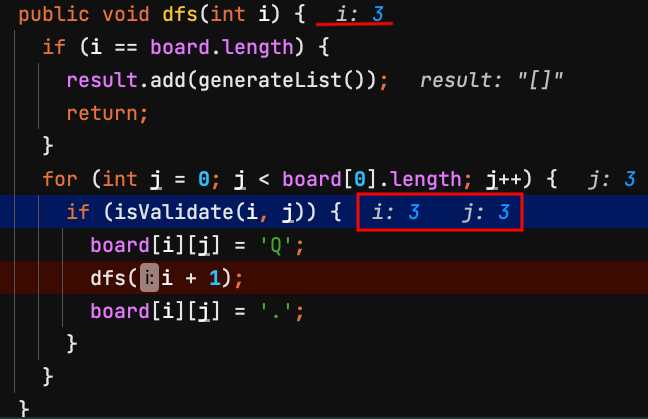
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 |
20.離開dfs(3),回到上一個dfs(2)方法,把第2列board[2][1]皇后移掉,變成預設值.。
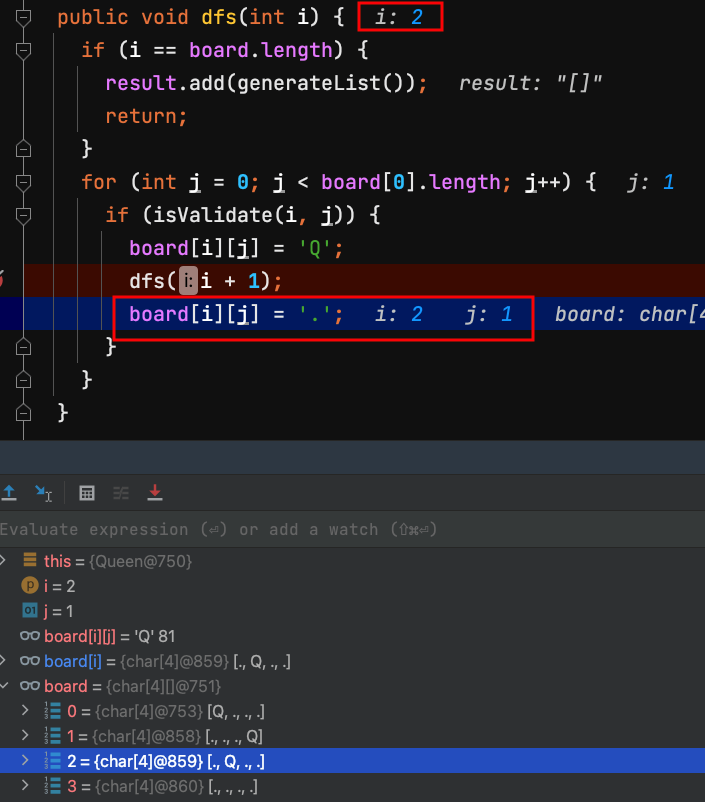
21.把第2列board[2][1]皇后移掉,變成預設值.
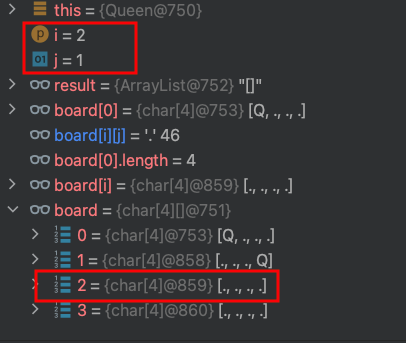
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
22.dfs(2) 第2列 row = 2,檢查board[2][2]是否能放皇后?不能,j換下一個。
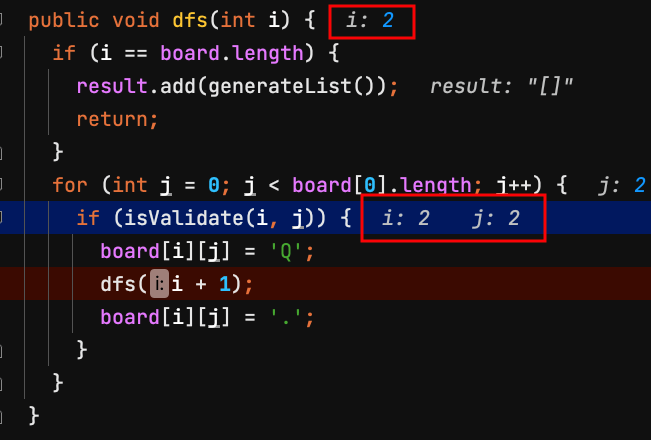
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
23.dfs(2) 第2列 row = 2,檢查board[2][3]是否能放皇后?不能,離開dfs(2)方法。。
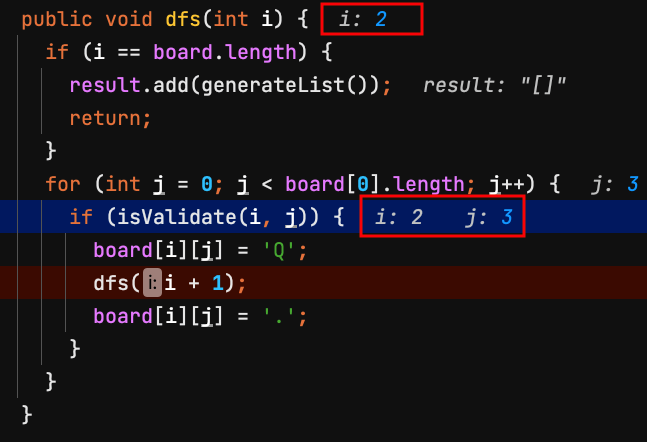
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
24.離開dfs(2),回到上一個dfs(1)方法,把第2列board[1][3]皇后移掉,變成預設值.。
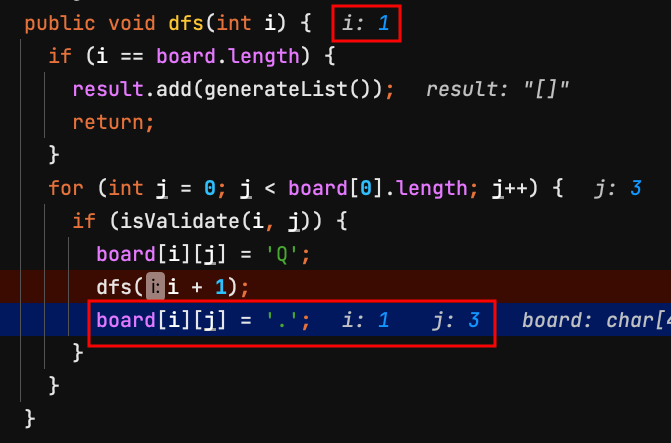
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
25.把第2列board[1][3]皇后移掉,變成預設值.。
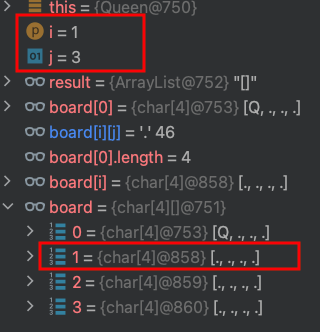
26.離開dfs(1),回到上一個dfs(0)方法,把第0列board[0][0]皇后移掉,變成預設值.。
由於放置皇后在(0,0),後面的列row都沒辦法有放置皇后的方法,所以回到最源頭,把(0,0)皇后撤銷。
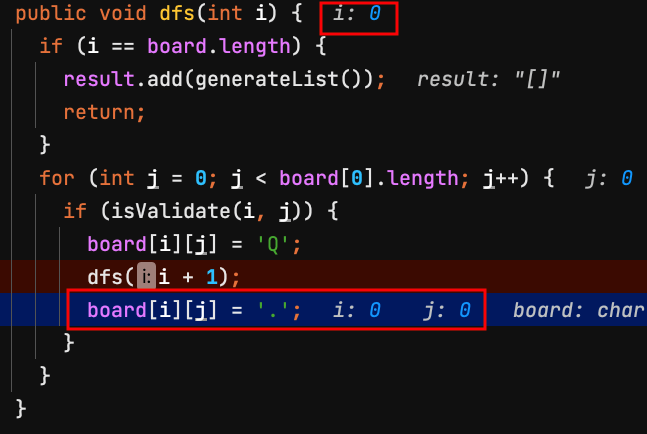
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | ||||
| i=1 | ||||
| i=2 | ||||
| i=3 |
27.dfs(0) 第0列 row = 0 ,把board[0][1]放一個Q,Q代表Queen皇后。
使用(0,0)失敗,改使用(0,1)試看看。
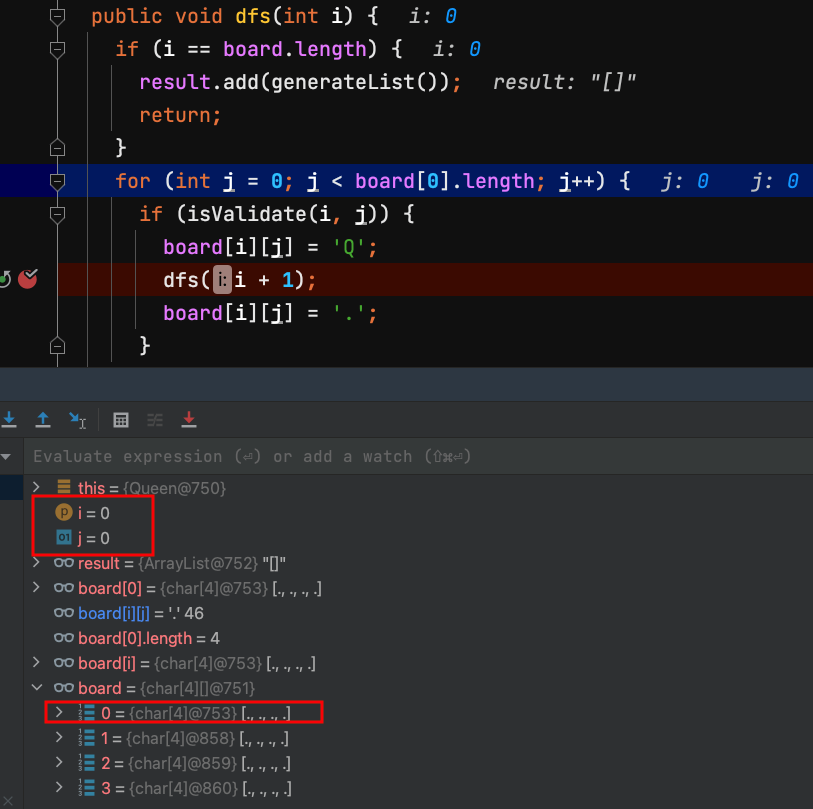
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | ||||
| i=2 | ||||
| i=3 |
28.board[0][1]放一個Q,Q代表Queen皇后。
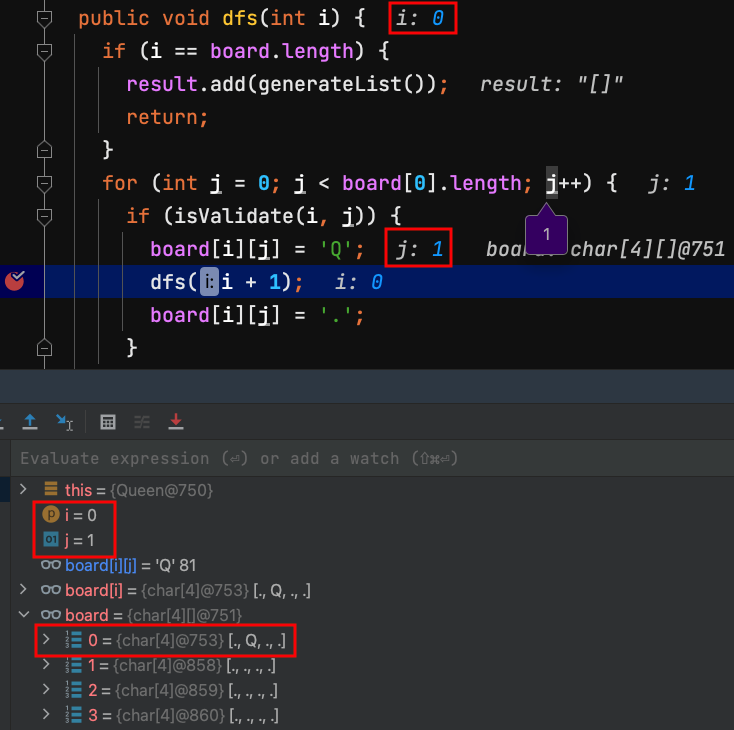
29.dfs(1) 第1列 row = 1 ,把board[1][3]放一個Q,Q代表Queen皇后。
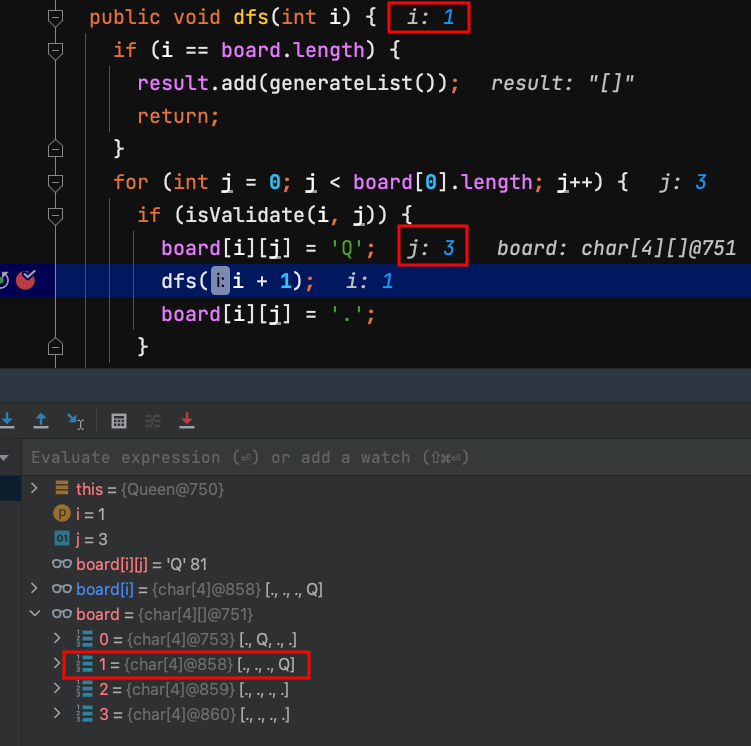
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | ||||
| i=3 |
30.dfs(2) 第2列 row = 2 ,把board[2][0]放一個Q,Q代表Queen皇后。
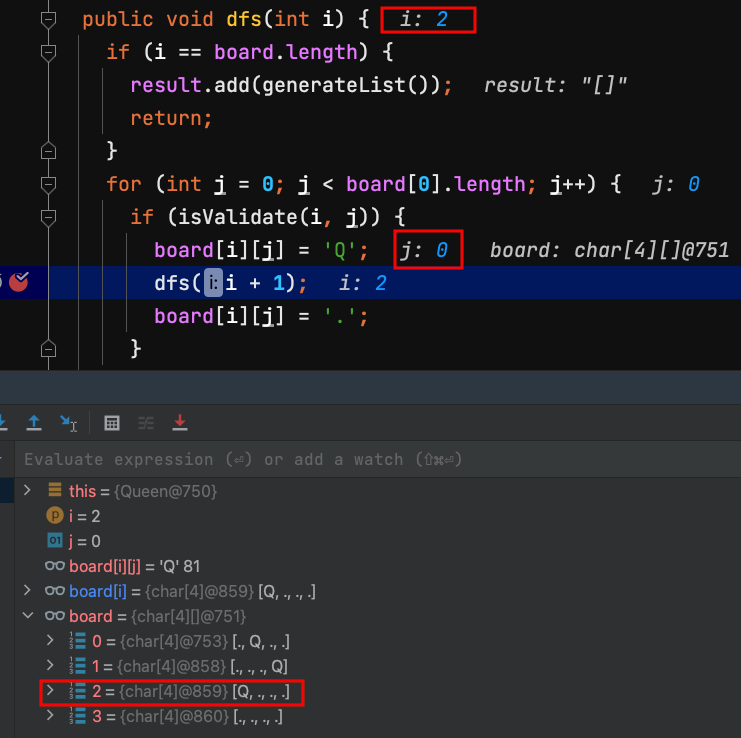
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 |
31.dfs(3) 第3列 row = 3 ,把board[3][2]放一個Q,Q代表Queen皇后。
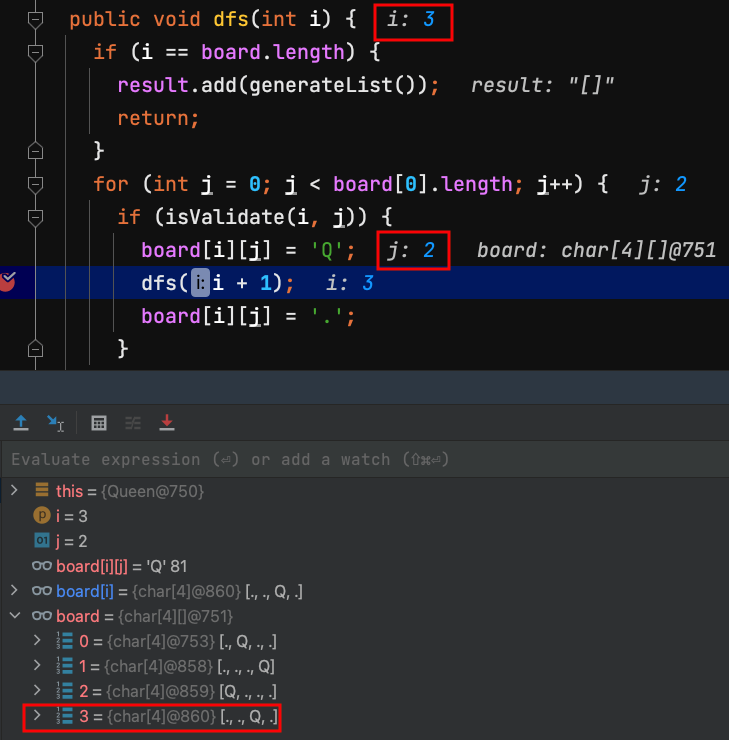
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | Q | |||
| i=1 | Q | |||
| i=2 | Q | |||
| i=3 | Q |
32.dfs(4) 當i=4,代表第0列row 至 第3列row,都成功放置皇后。
i == 4,離開遞迴的條件,把棋盤皇后放置的位置儲存到result,返回上一個方法dfs(3)。
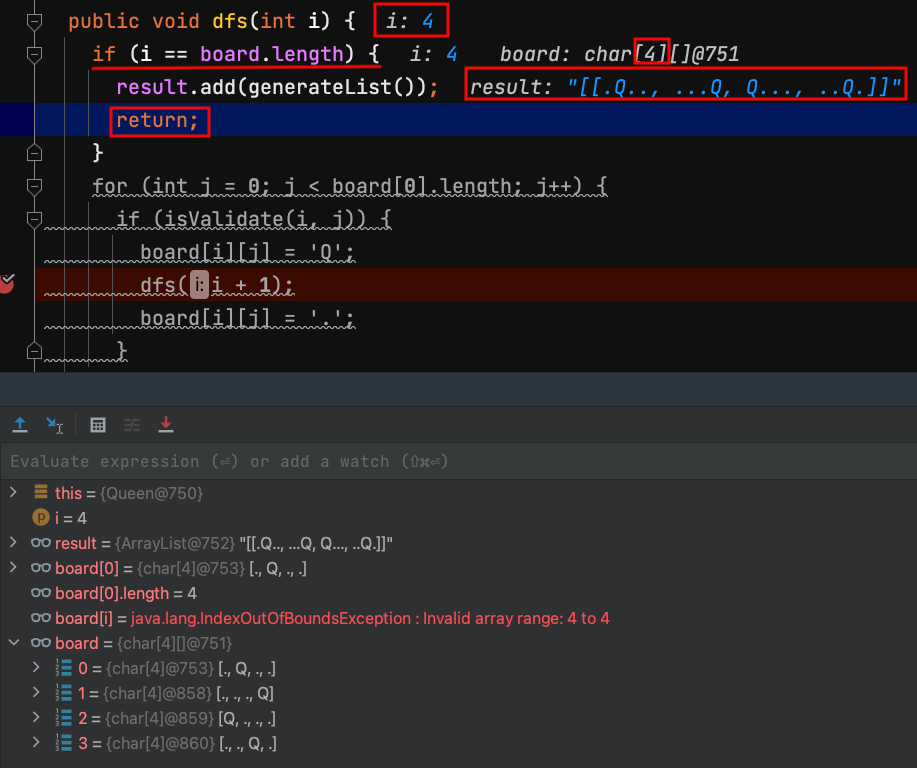
33.dfs(3) 把第3列皇后撤銷。
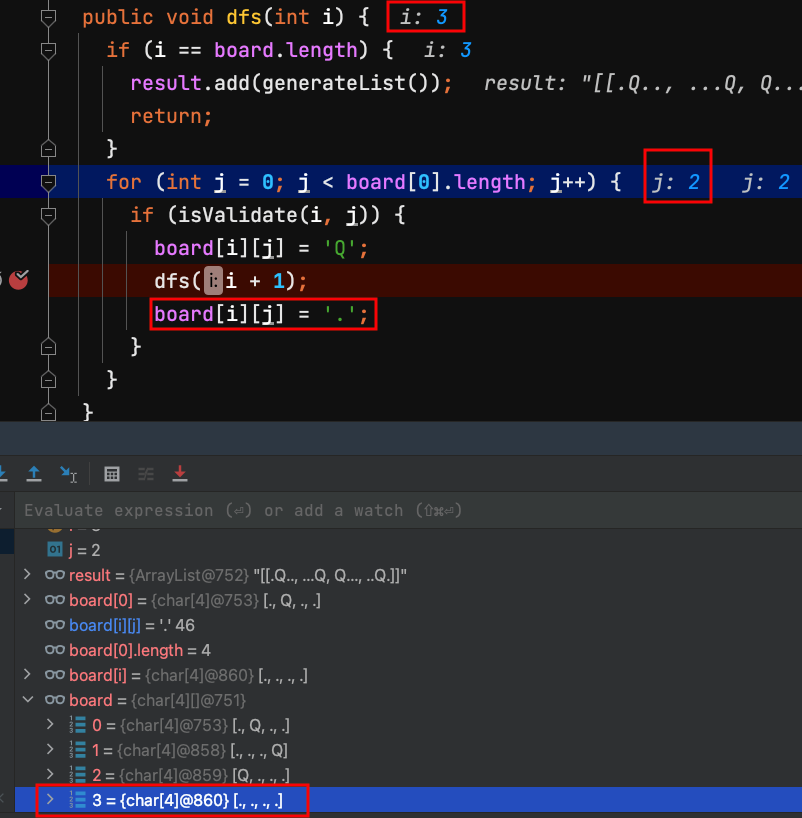
34.dfs(2) 把第2列皇后撤銷。
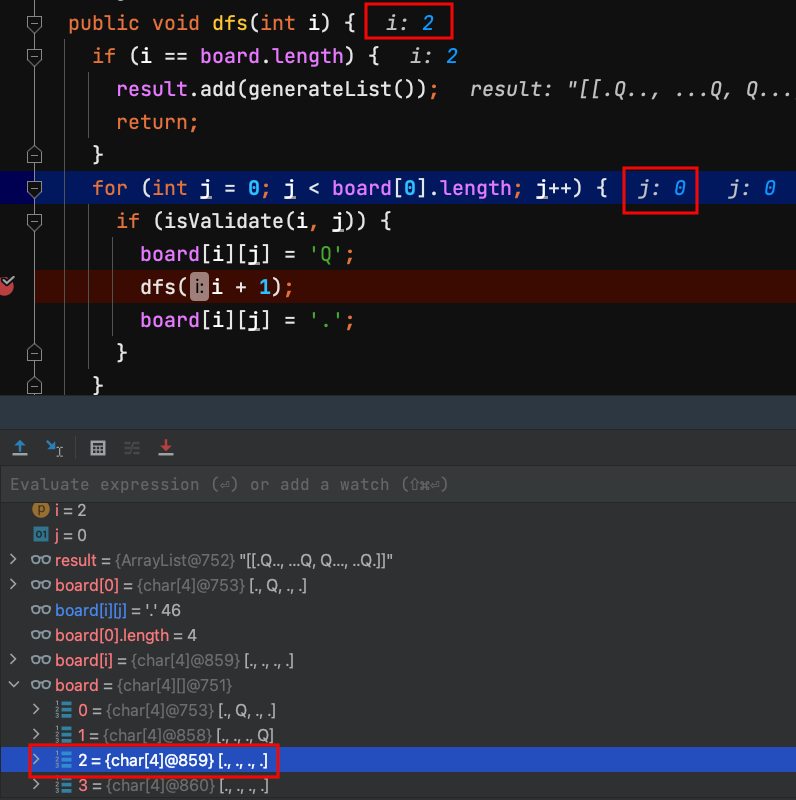
35.dfs(1) 把第1列皇后撤銷。
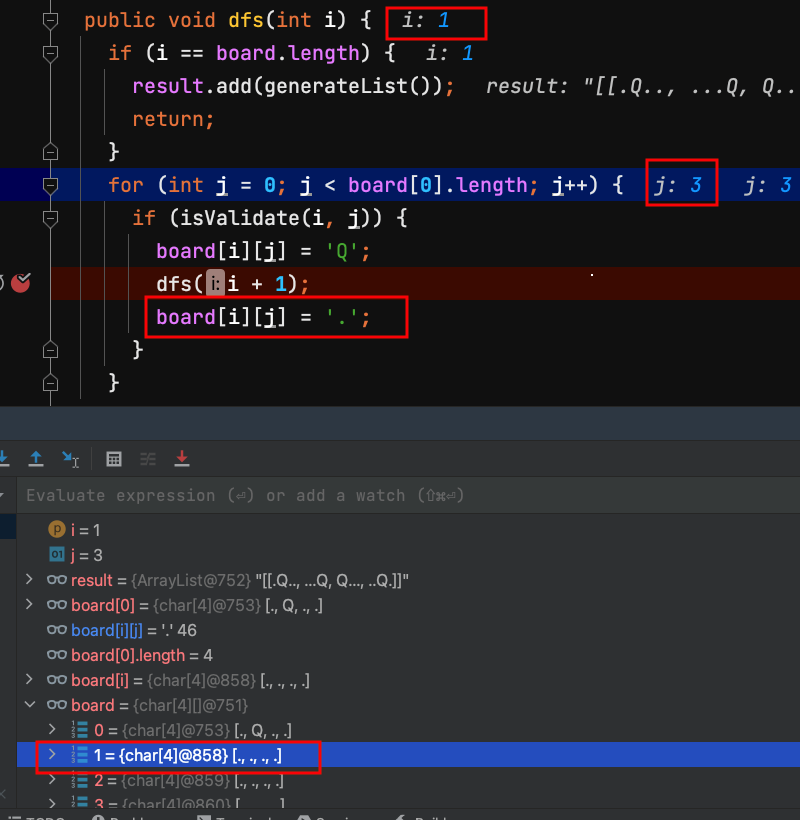
36.dfs(0) 把第0列皇后撤銷。
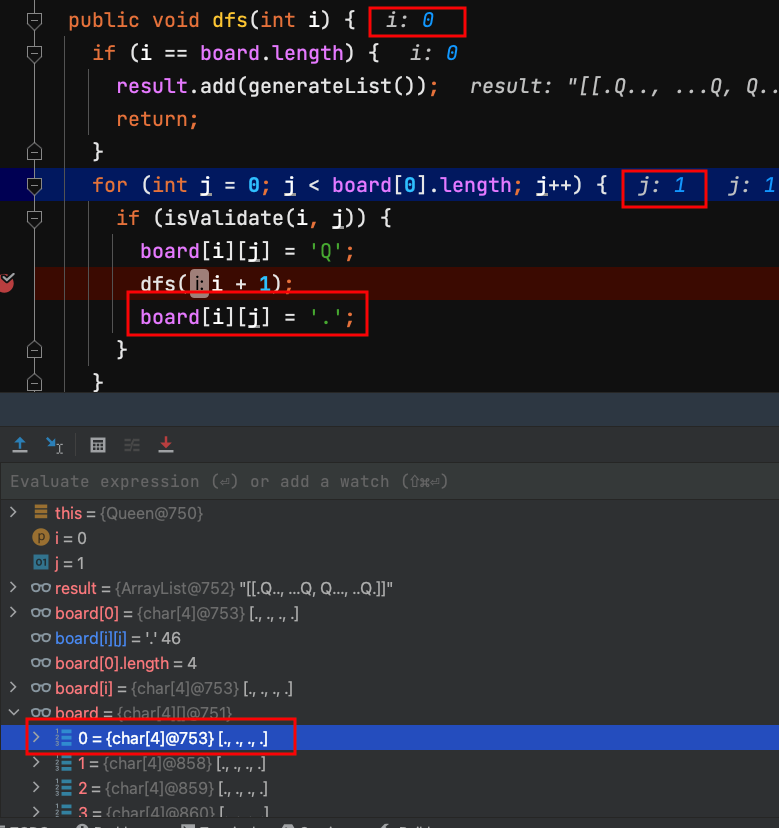
皇后全撤銷掉,再從(0,3)與(0,4)探尋其它放置皇后的可能。
完整程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Queen {
// 準備棋盤
private char[][] board;
// 4乘4大小的棋盤
private int N = 4;
public Queen() {
// 建立棋盤
board = new char[N][N];
// 預設字元陣列都是點.
for (int i = 0; i < board.length; i++) {
Arrays.fill(board[i],'.');
}
}
// 參數 i為列row,針對每一列row,放皇后
public void dfs(int i, List<List<String>> result) {
// 如果 i == 4,代表上一次遞迴是dfs(3)
// dfs(3) row=3 i=3,代表第3列的皇后成功放置了,才會呼叫dfs(4)
// 注意!不是i == board.length - 1,沒有減1
// 把第0-3列的所有皇后放法存在List中,並離開遞迴,返回dfs(3)
if (i == board.length) {
List<String> list = new ArrayList<String>();
for (char[] row: board) {
// 把字串陣列轉成String存到List中
list.add(new String(row)) ;
}
result.add(list);
return; // 返回dfs(3)
}
// j代表column,對每一欄嘗試放置皇后
for (int j = 0; j < board[0].length; j++) {
// 檢查欄 左斜 右斜 是否有放其它皇后
if (isValidate(i, j)) {
// 放皇后
board[i][j] = 'Q';
// dfs(下一列row) 下一列放皇后
dfs(i + 1, result);
// 找到皇后放置的方法,會回到此處dfs(3),清空皇后
// 一路返回dfs(2) -> 清空皇后 -> dfs(1) -> 清空皇后 -> dfs(0) -> 清空皇后
// 清空皇后後,再尋找新的放置皇后的路徑。
// 撤銷皇后也會回到此處
board[i][j] = '.';
}
}
}
// 參數 列row與欄column,檢查是否能放皇后
public boolean isValidate(int row, int col) {
// 檢查每一列row,在同一欄是否有皇后
for (int i = 0; i <= row; i++) {
if (board[i][col] == 'Q') {
return false;
}
}
// i與j的初始值是(row - 1, col - 1),假設(row=3,col=3)
// 就會變成(2,2),也就是上面左斜,持續減1
// (3,3) -> (2,2) -> (1,1) -> (0,0)
// 由於遞迴只會造成上面的列數要檢查,所以不考慮下面的列
// 不能減到超出棋盤邊界,不能為-1
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') {
return false;
}
}
// i與j的初始值是(row - 1, col + 1),假設(row=3,col=0)
// 就會變成(2,1),也就是上面右斜,持續往上右斜檢查
// (3,0) -> (2,1) -> (1,2)
// 由於遞迴只會造成上面的列數要檢查,所以不考慮下面的列
// 不能減到超出棋盤邊界,不能為-1,也不能col + 1,加到超出board.length
for (int i = row - 1, j = col + 1; i >=0 && j < board.length; i--, j++) {
if (board[i][j] == 'Q') {
return false;
}
}
return true;
}
public static void main(String[] args) {
Queen queen = new Queen();
List<List<String>> result = new ArrayList<>();
// 從第0列 row = 0 放置皇后
queen.dfs(0, result);
System.out.println(result);
}
}
[[.Q.., ...Q, Q..., ..Q.], [..Q., Q..., ...Q, .Q..]]