BFS
預先準備
- matrix二維陣列,1代表連起來(Connected),0代表不能連。
visted[]陣列,判斷是否已訪問過。- Queue佇列
matrix二維陣列:
| 頂點 | j=0 | j=1 | j=2 | j=3 |
| i=0 | 0 | 1 | 1 | 0 |
| i=1 | 1 | 0 | 0 | 1 |
| i=2 | 1 | 0 | 0 | 0 |
| i=3 | 0 | 1 | 0 | 0 |
visted陣列
| 頂點 | 0 | 1 | 2 | 3 |
| visted | F | F | F | F |
先把頂點0放入佇列,下圖中,箭頭入是放入佇列的方向,箭頭出是從佇列取出的方向。
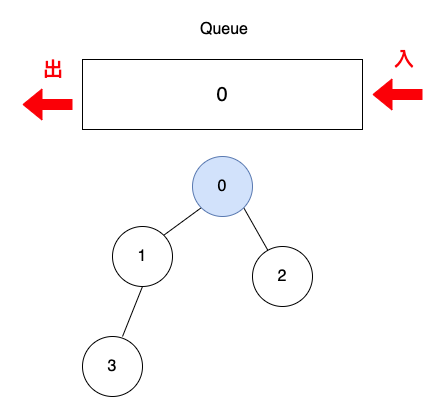
把頂點設為已訪問,避免重覆訪問。
| 頂點 | 0 | 1 | 2 | 3 |
| visted | F | F | F |
把頂點0從佇列取出來,印出頂點0。
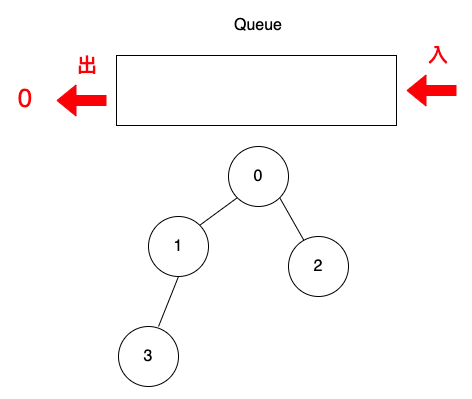
查一下matrix表格中,第0列(i=0)代表頂點0,j是相連頂點,1代表相連,j=1與j=2的時候,是1,是相連的,把頂點1與頂點2放入佇列。
| 頂點 | j=0 | j=1 | j=2 | j=3 |
| i=0 | 0 | 1 | 1 | 0 |
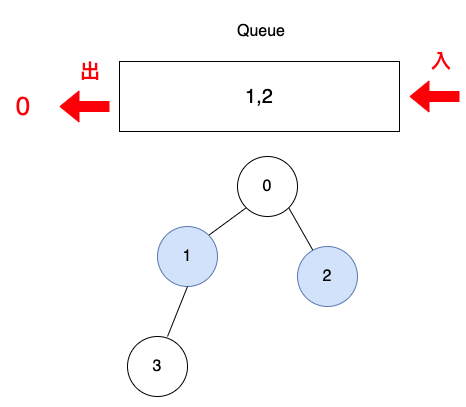
並把頂點1與頂點2設為已訪問。
| 頂點 | 0 | 1 | 2 | 3 |
| visted | T | F |
把頂點1從佇列取出,印出頂點1。
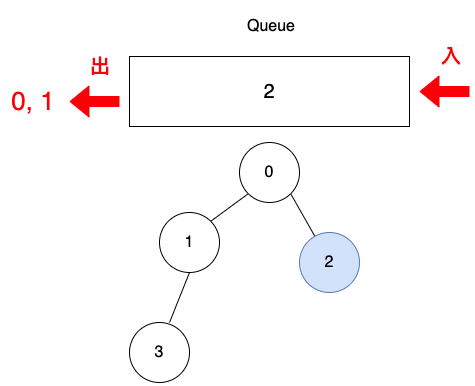
查一下matrix表格中,第1列(i=1)代表頂點1,j是相連頂點,1代表相連,j=0與j=3的時候,是1,是相連的,但頂點0已被訪問過,只放入未訪問頂點3放入佇列。
| 頂點 | j=0 | j=1 | j=2 | j=3 |
| i=0 | 0 | 1 | 1 | 0 |
| i=1 | 1 | 0 | 0 | 1 |
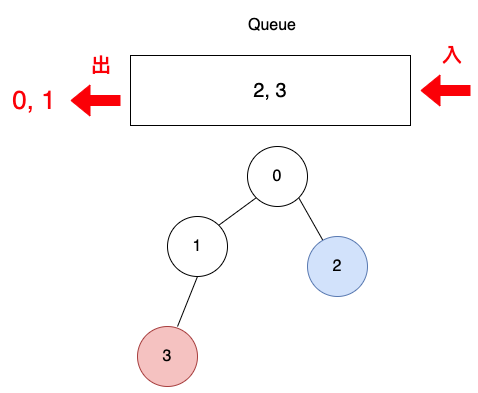
並把頂點3設為已訪問。
| 頂點 | 0 | 1 | 2 | 3 |
| visted | T | T | T |
把頂點2從佇列取出,印出頂點2。
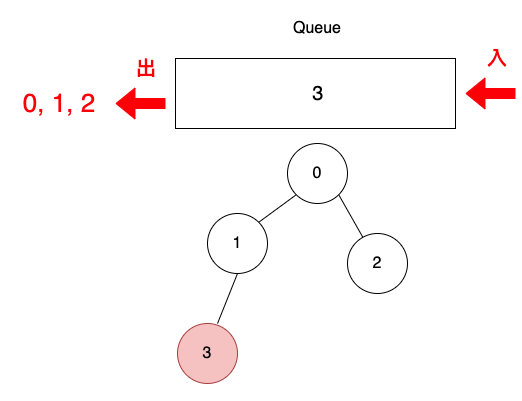
把頂點3從佇列取出,印出頂點3。
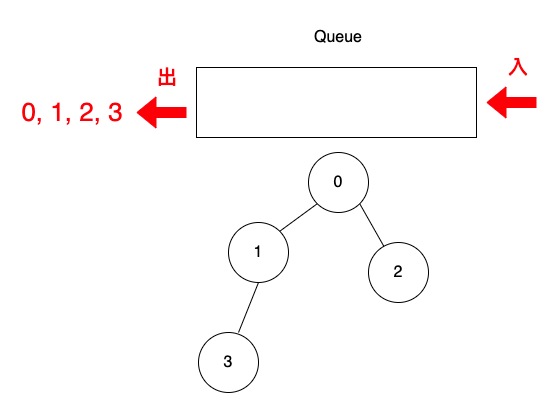
完整程式碼如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import java.util.LinkedList;
public class BFS {
private int[][] matrix;
private int vertexLen = 4;
private boolean[] visted;
public BFS() {
matrix = new int[vertexLen][vertexLen];
matrix[0] = new int[]{0, 1, 1, 0};
matrix[1] = new int[]{1, 0, 0, 1};
matrix[2] = new int[]{1, 0, 0, 0};
matrix[3] = new int[]{0, 1, 0, 0};
visted = new boolean[vertexLen];
}
public void bfs() {
LinkedList<Integer> queue = new LinkedList<>();
// 因為可能會有頂點互相不連通,所以要使用for,確保每個頂點都訪問到。
for (int i = 0; i < vertexLen; i++) {
// 是否訪問過?
if (!visted[i]) {
// 沒訪問過才加入queue
queue.add(i);
// 設為已訪問
visted[i] = true;
}
// 若queue不為空就一直迴圈
while (!queue.isEmpty()) {
// 從queue取出頂點
int vertex = queue.poll();
// 印出頂點
System.out.print(vertex + "->");
// 檢查j欄(column)的頂點是否有相連
for (int j = 0; j < vertexLen; j++) {
// 沒有被訪問 並且相連
if (!visted[j] && matrix[vertex][j] == 1) {
// 加入queue
queue.add(j);
// 設為已訪問
visted[j] = true;
}
}
}
}
}
public static void main(String[] args) {
BFS bfs = new BFS();
bfs.bfs();
}
}
0->1->2->3->
一層層遍歷
上面的程式碼,是頂點加入Queue,頂點從Queue取出,尋找跟此頂點相鄰的邊,再把相鄰的頂點加入Queue,Queue不為空,再從Queue取出頂點,尋找跟此頂點相鄰的邊,再把相鄰的頂點加入Queue,如此反覆遍歷,直到Queue為空。
如果需要知道經過幾層,才能遍歷完畢?
加入頂點0,頂點0是第1層。
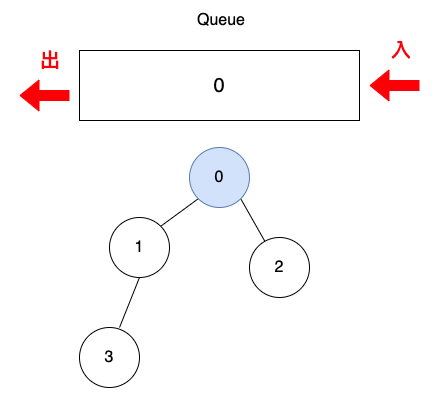
取出頂點0。
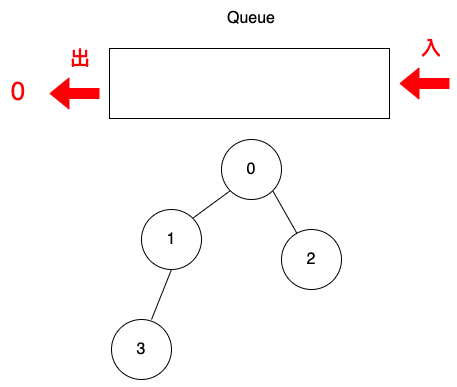
加入頂點1與2,頂點1與2是第2層。
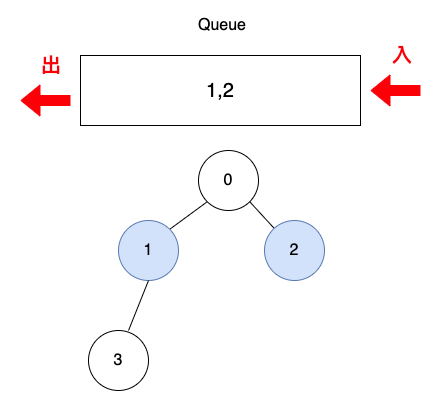
取出頂點1與2,取出1的過程檢查出1的相鄰頂點3,把頂點3加入queue。
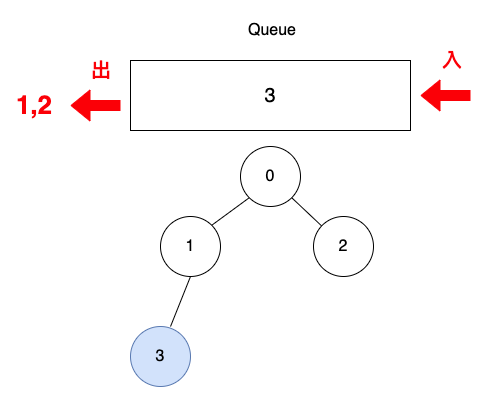
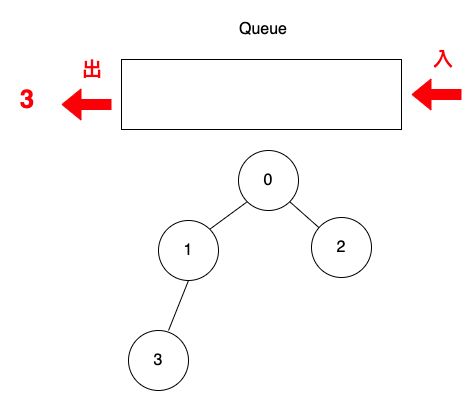
取出頂點3,頂點3是第3層。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public void bfsLayer() {
LinkedList<Integer> queue = new LinkedList<>();
// 記錄層數
int layer = 0;
// 從頂點0開始,此圖為連通圖,沒有不連通或孤立的圖
int start = 0;
queue.add(start);
// 設已訪問
visted[start] = true;
while (!queue.isEmpty()) {
// 每一層有多少頂點
int size = queue.size();
// 增加一層
layer++;
// 針對每一層的頂點進行for循環
for (int cnt = 0; cnt < size; cnt++) {
int vertex = queue.poll();
System.out.print(vertex + "->");
for (int j = 0; j < vertexLen; j++) {
if (!visted[j] && matrix[vertex][j] == 1) {
queue.add(j);
visted[j] = true;
}
}
}
}
System.out.println();
System.out.println("layer = " + layer);
}
0->1->2->3->
layer = 3