拓樸排序
拓樸排序,是根據分支度小的先排序。
所謂的分支度,在無向圖中,是一個頂點連接的邊的總數。
拓樸排序針對無迴路的圖才能運作,下圖是有迴路的圖,無法使用拓樸排序,但可以透過拓樸排序檢查出是否有迴路。
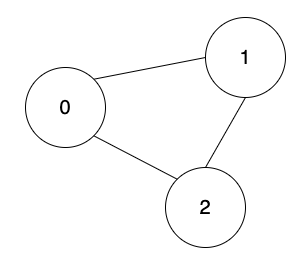
無向圖
所謂的分支度,在無向圖中是多少條邊edge連到頂點的數量。
下圖中,頂點0有1條邊連著,頂點1有2條邊連著,頂點2有1條邊連著,這連著的邊就是分支度。
無向圖中,最小的分支度是1,因為頂點與頂點連接至少會有一條邊。
拓樸排序(無向圖),是將分支度為1的頂點放入Queue中,逐一刪掉,和刪除頂點「相鄰頂點」的「邊」,也要跟著一起刪掉,若相鄰頂點刪掉的邊在無向圖中,只剩下1條邊(無向圖中分支度最小單位),則加入Queue中,排隊刪除。
分支度
分支度的統計可以列(row)的方式統計。
| j=0 | j=1 | j=2 | 分支度 | |
| i=0 | 0 | 1 | 0 | 1 |
| i=1 | 1 | 0 | 1 | 2 |
| i=2 | 0 | 1 | 0 | 1 |
分支度的統計可以欄(column)的方式統計。
| j=0 | j=1 | j=2 | |
| i=0 | 0 | 1 | 0 |
| i=1 | 1 | 0 | 1 |
| i=2 | 0 | 1 | 0 |
| 分支度 | 1 | 2 | 1 |
準備
準備degree陣列,記錄每個頂點的分支度(連著頂點的邊)的數量,大小為頂點的數量。
| 頂點 | 0 | 1 | 2 |
| 分支度 | 1 | 2 | 1 |
步驟
分支度小的頂點先從圖中把邊刪掉,其它跟它相連的頂點,也要把他們的分支度減1,直到所有頂點都訪問完畢,代表遍歷完成。
1.接下來把所有degree等於1的頂點放入Queue。
degree等於1,代表只有一條邊連著,由最少的邊開始。
把degree為1的頂點0與2放入Queue中。
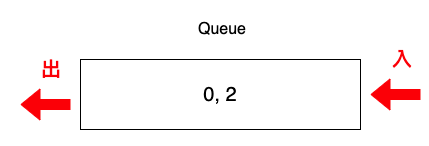
2.把Queue 中的元素拿出來,首先拿到的是0(先入先出)。
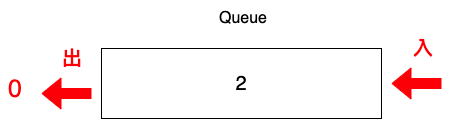
3.刪除頂點0。
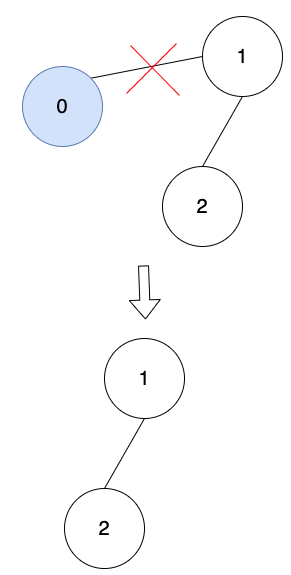
並輸出在螢幕。
0,
4.因為頂點0已被刪掉,跟頂點0有連接的鄰居們,鄰居跟頂點0有連線的邊也要刪掉1條。
| 頂點 | 0 | 1 | 2 |
| 分支度 | 1 | 1 |
頂點1刪掉的degree剩下1,把頂點1加入Queue。
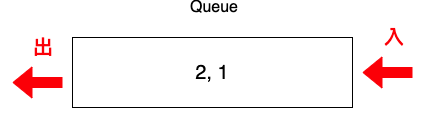
5.把Queue中的頂點2拿出來,刪除頂點2。
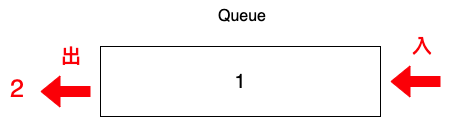
並輸出在螢幕。
0, 2
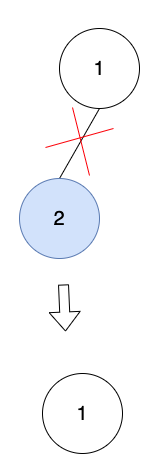
6.因為頂點2已被刪掉,跟頂點2有連接的鄰居們,鄰居跟頂點2有連線的邊也要刪掉1條。
| 頂點 | 0 | 1 | 2 |
| 分支度 | 1 | 1 |
7.把Queue中的頂點1拿出來,刪除頂點1。
並輸出在螢幕。
0, 2, 1
8.Queue已經沒有元素,拓樸排序遍歷完成。
程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
public class Topology {
// 相鄰矩陣
private int[][] matrix;
// 頂點數量
private int vertexLen = 3;
// 分支度
private int[] degree;
public int getVertexLen() {
return vertexLen;
}
public Topology() {
matrix = new int[vertexLen][vertexLen];
// 1代表連著的邊,0代表沒有連
matrix[0] = new int[]{0, 1, 0};
matrix[1] = new int[]{1, 0, 1};
matrix[2] = new int[]{0, 1, 0};
degree = new int[vertexLen];
for (int i = 0; i < vertexLen; i++) {
for (int j = 0; j < vertexLen; j++) {
if (matrix[i][j] == 1) {
// 以列(row)的方式統計分支度
degree[i]++;
}
}
}
}
public int topology() {
LinkedList<Integer> queue = new LinkedList<Integer>();
// 計算刪除頂點數量
int vistedCnt = 0;
for (int i = 0; i < degree.length; i++) {
// degree == 1就加入queue
if (degree[i] == 1) {
queue.add(i);
}
}
while (!queue.isEmpty()) {
// 從queue取出頂點,代表刪除該頂點
int vertex = queue.poll();
// 計算刪除頂點數量 +1
vistedCnt++;
// 印出
System.out.print(vertex + ",");
// 檢查是否有相鄰的頂點
for (int j = 0; j < vertexLen; j++) {
// 有相鄰的頂點j,分支度要減1
if (matrix[vertex][j] == 1) {
degree[j]--;
// degree == 1就加入queue
if (degree[j] == 1) {
queue.add(j);
}
}
}
}
System.out.println();
return vistedCnt;
}
public static void main(String[] args) {
Topology topology = new Topology();
int visitedCnt = topology.topology();
// 若刪掉的頂點數量跟實際的頂點數量一樣,代表沒有迴路
System.out.println("hasCircle ? " + (visitedCnt != topology.vertexLen));
}
}
0,2,1,
hasCircle ? false
判斷無向圖是否有迴路
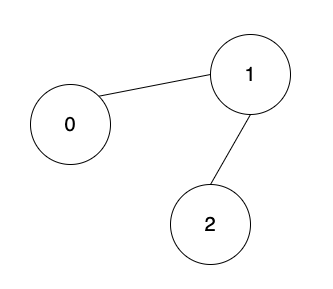
下圖中,頂點0有2條邊連著,頂點1有2條邊連著,頂點2有2條邊連著,這連著的邊就是分支度。

分支度
分支度的統計可以列(row)的方式統計。
| j=0 | j=1 | j=2 | 分支度 | |
| i=0 | 0 | 1 | 1 | 2 |
| i=1 | 1 | 0 | 1 | 2 |
| i=2 | 1 | 1 | 0 | 2 |
分支度的統計可以欄(column)的方式統計。
| j=0 | j=1 | j=2 | |
| i=0 | 0 | 1 | 1 |
| i=1 | 1 | 0 | 1 |
| i=2 | 1 | 1 | 0 |
| 分支度 | 2 | 2 | 2 |
如果要判斷無向圖,是否「有迴路」,除了union find可判斷是否有迴路,拓撲排序也可以判斷圖中是否有迴路。
判斷迴路
1.準備degree陣列,記錄每個頂點的分支度,大小為頂點的數量。
| 頂點 | 0 | 1 | 2 |
| 分支度 | 2 | 2 | 2 |
3.發現根本沒有頂點的分支度是1,所以沒有一個頂點加到Queue中。
4.刪除的頂點數量跟實際的頂點數量不符,代表有迴路。
直接把先前的程式中的相鄰矩陣改成有迴路。
1
2
3
4
matrix = new int[vertexLen][vertexLen];
matrix[0] = new int[]{0, 1, 1};
matrix[1] = new int[]{1, 0, 1};
matrix[2] = new int[]{1, 1, 0};
有向圖
有向圖中,只在乎「入」分支度。什麼是入分支度?就是箭頭指向頂點的邊的數量。
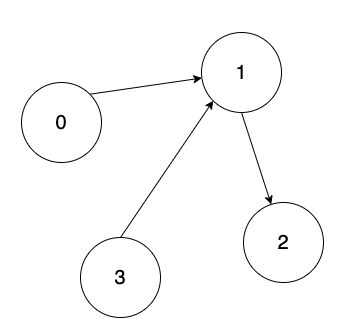
有向圖,是根據入分支度為0的先排序,0是沒有箭頭指向,先處理沒有任何箭頭指向的頂點。
拓樸排序(有向圖),是將入分支度為0的頂點放入Queue中,逐一刪掉,和刪除頂點「相鄰頂點」的「入分支度」,也要跟著一起刪掉,若相鄰頂點刪掉的入分支度為0條(有向圖中入分支度最小單位),則加入Queue中,排隊刪除。
入分支度
i代表從i頂點,箭頭指向j。
i代表「出」邊,箭頭從i頂點出去,j代表「入」邊,箭頭指向j頂點。
所以入分支度的統計,以column欄,箭頭指向的j為主,垂直統計有多少頂點指向自己。
| j=0 | j=1 | j=2 | j=3 | |
| i=0 | 0 | 1 | 0 | 0 |
| i=1 | 0 | 0 | 1 | 0 |
| i=2 | 0 | 0 | 0 | 0 |
| i=3 | 0 | 1 | 0 | 0 |
| 入分支度 | 0 | 2 | 1 | 0 |
| 頂點 | 0 | 1 | 2 | 3 |
| 入分支度 | 0 | 2 | 1 | 0 |
所謂的出邊,也稱出分支度,從i頂點「出發」,箭頭指向其它頂點,也就是從i頂點出發的個數,水平統計有多少邊指向其它頂點。
對i頂點而言是出邊,但對j頂點而言是入邊,由i頂點的出邊反推回j頂點的入邊。
| j=0 | j=1 | j=2 | j=3 | 出分支度 | |
| i=0 | 0 | 1 | 0 | 0 | 1 |
| i=1 | 0 | 0 | 1 | 0 | 1 |
| i=2 | 0 | 0 | 0 | 0 | 0 |
| i=3 | 0 | 1 | 0 | 0 | 1 |
| 頂點 | 0 | 1 | 2 | 3 |
| 出分支度 | 1 | 1 | 0 | 1 |
與先前程式碼大同小異,主要是相鄰矩陣「入分支度」的統計。
入分支度為0(代表沒有頂點指向自己),加入Queue,從最少的入分支度開始。
還有要把Queue中i頂點從圖上刪除,要找從i出發的出邊,推斷出j頂點的入分支度,並將j頂點的入分支度減1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
public class InDegreeTopology {
// 相鄰矩陣
private int[][] matrix;
// 頂點數量
private int vertexLen = 4;
// 入分支度
private int[] indegree;
public int getVertexLen() {
return vertexLen;
}
public InDegreeTopology() {
matrix = new int[vertexLen][vertexLen];
// 1代表連著的邊,0代表沒有連
matrix[0] = new int[]{0, 1, 0, 0};
matrix[1] = new int[]{0, 0, 1, 0};
matrix[2] = new int[]{0, 0, 0, 0};
matrix[3] = new int[]{0, 1, 0, 0};
indegree = new int[vertexLen];
for (int i = 0; i < vertexLen; i++) {
for (int j = 0; j < vertexLen; j++) {
if (matrix[i][j] == 1) {
// 入分支度以j為主,有多少箭頭指向此頂點
indegree[j]++;
}
}
}
//System.out.println(Arrays.toString(indegree));
}
public int topology() {
LinkedList<Integer> queue = new LinkedList<>();
// 計算刪除頂點數量
int vistedCnt = 0;
for (int i = 0; i < indegree.length; i++) {
// 入分支度為0,代表沒有頂點指向
if (indegree[i] == 0) {
// 加入queue
queue.add(i);
}
}
// 迴圈進入的條件,queue不為空
while (!queue.isEmpty()) {
// 從queue取出頂點,代表刪除該頂點
int vertex = queue.poll();
// 計算刪除頂點數量 +1
vistedCnt++;
// 印出頂點
System.out.print(vertex + ", ");
// 檢查是否有出邊,也就是箭頭指向其它頂點
for (int j = 0; j < vertexLen; j++) {
// 箭頭指向其它頂點
if (matrix[vertex][j] == 1) {
// 把那個頂點入分支度減1
indegree[j]--;
// 若那個頂點入分支度為0,代表沒人指向它
if (indegree[j] == 0) {
// 加入queue
queue.add(j);
}
}
}
}
System.out.println();
return vistedCnt;
}
public static void main(String[] args) {
InDegreeTopology inDegreeTopology = new InDegreeTopology();
int vistedCnt = inDegreeTopology.topology();
// 若刪掉的頂點數量跟實際的頂點數量一樣,代表沒有迴路
System.out.println("hasCircle = " + (vistedCnt != inDegreeTopology.vertexLen));
}
}
0, 3, 1, 2,
hasCircle = false
尋找樹的中心,最小高度樹
奇數個數頂點
假設有長長的樹
0 - 1 - 2 - 3 - 4
若0當根節點,高度為4。
若1當根節點,高度為3。
若2當根節點,高度為2。
2當根節點就是最小高度的樹。
如何求出樹的中心?
要把最外圍的頂點先刪除。
0 - 1 - 2 - 3 - 4
先刪掉0與4頂點。
1 - 2 - 3
再刪掉1與3頂點。
2
偶數個數頂點
若頂點是偶數。
0 - 1 - 2 - 3 - 4 - 5
先刪掉0與5頂點。
1 - 2 - 3 - 4
再刪掉1與4頂點。
2 - 3
剩下頂點2與頂點3,就是中心頂點。
奇數圖
要使用到bfs層層遍歷,先把最外層,分支度為1的頂點刪掉,紅色框框代表是同一層。
最後刪掉的那一層,就是中心頂點。
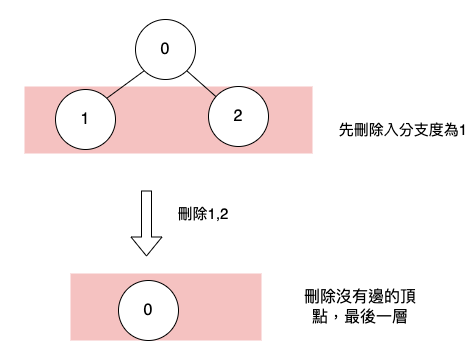
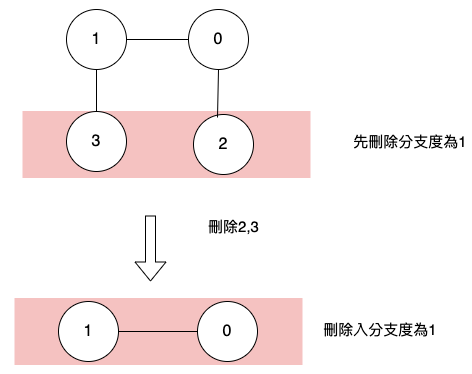
偶數圖
要使用到bfs層層遍歷,先把最外層,分支度為1的頂點刪掉,紅色框框代表是同一層。
最後刪掉的那一層,就是中心頂點。
程式碼
bfs使用層層遍歷,最後那一層,就是中心頂點。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
public class MiniHightTree {
// 相鄰矩陣
private int[][] matrix;
// 頂點數量
private int vertexLen = 3;
// 分支度
private int[] degree;
public int getVertexLen() {
return vertexLen;
}
public MiniHightTree() {
matrix = new int[vertexLen][vertexLen];
// 1代表連著的邊,0代表沒有連
matrix[0] = new int[]{0, 1, 0};
matrix[1] = new int[]{1, 0, 1};
matrix[2] = new int[]{0, 1, 0};
degree = new int[vertexLen];
for (int i = 0; i < vertexLen; i++) {
for (int j = 0; j < vertexLen; j++) {
if (matrix[i][j] == 1) {
// 以列(row)的方式統計分支度
degree[i]++;
}
}
}
}
public List<Integer> getMiniHightRoot() {
// 記錄刪到最後,最後一層頂點
List<Integer> list = null;
LinkedList<Integer> queue = new LinkedList<Integer>();
// 計算刪除頂點數量
int vistedCnt = 0;
for (int i = 0; i < degree.length; i++) {
// degree == 1就加入queue
if (degree[i] == 1) {
queue.add(i);
}
}
while (!queue.isEmpty()) {
// 取出每一層的頂點個數
int size = queue.size();
// 每遍歷一層,list都會被清空,只記錄最後一層的頂點
list = new ArrayList<>();
// 遍歷這一層的頂點
for (int i = 0; i < size; i++) {
// 從queue取出頂點,代表刪除該頂點
int vertex = queue.poll();
// 計算刪除頂點數量 +1
vistedCnt++;
list.add(vertex);
// 檢查是否有相鄰的頂點
for (int j = 0; j < vertexLen; j++) {
// 有相鄰的頂點j,分支度要減1
if (matrix[vertex][j] == 1) {
degree[j]--;
// degree == 1就加入queue
if (degree[j] == 1) {
queue.add(j);
}
}
}
}
}
// 傳回最後一層的頂點
return list;
}
public static void main(String[] args) {
MiniHightTree topology = new MiniHightTree();
List result = topology.getMiniHightRoot();
System.out.println(result);
}
}
[1]